В ) Уравнение прямой, заданной точкой и вектором нормали.
Определение. Вектор перпендикулярный плоскости α называется вектором нормали плоскости α.
Очевидно, что существует множество векторов нормали для конкретной прямой,все они коллинеарны между собой.
Задача составления уравнения прямой, заданной точкой и вектором нормали, является метрической задачей. Метрические задачи обычно рассматриваются в прямоугольной системе координат.
Введём на плоскости прямоугольную систему координат R(O,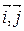 
). В которой зададим точку М0, вектор 
и рассмотрим прямую, проходящую через точку М0 перпендикулярно вектору 
.
Рис. 11
Очевидно, что произвольная точка М принадлежит прямой ℓ тогда и только тогда когда 
. Условием перпендикулярности векторов является равенство нулю их скалярного произведения. Учитывая то, что 
получаем:
|
(9)
Уравнение (9) называется уравнением плоскости, заданной точкой Мо(хо,уо) и вектором нормали .
Лекция №3