Излучение происходит только при перескоке электрона с одной стационарной орбиты на другую.
Теперь обратимся к экспериментальным фактам. Если сильно разогреть газ, как это происходит в водородной лампе, то атом поглощает часть энергии. При этом электрон скачком переходит с нижней стационарной орбиты (уровня, оболочки - это одно и то же) на более высокие стационарные орбиты (уровни, оболочки). Такой "возбужденный" атом не может долго существовать и электрон возвращается ("падает") на более низкую орбиту, выделяя при этом строго определенную порцию (квант) световой энергии. Поскольку орбит в атоме конечное число, в спектре испускаемого водородной лампой света наблюдаются не плавные переходы от одного цвета к другому, а лишь отдельные линии на черном фоне (рис.2-13) - это и есть линейчатый спектр. Число линий должно совпадать с числом электронных переходов между стационарными орбитами.
Например, переход электрона с одного из высоких уровней на 2-й уровень сопровождается выделением отдельных "порций" световой энергии - квантов света в видимой области. Переходы между близко расположенными уровнями дают менее энергичные кванты красного цвета. Наиболее энергичные (ультрафиолетовые) кванты выделяются при возврате электрона на ближайший к ядру 1-й уровень. Кванты одного вида сливаются вместе и наблюдаются в спектрометре в виде тонких линий.
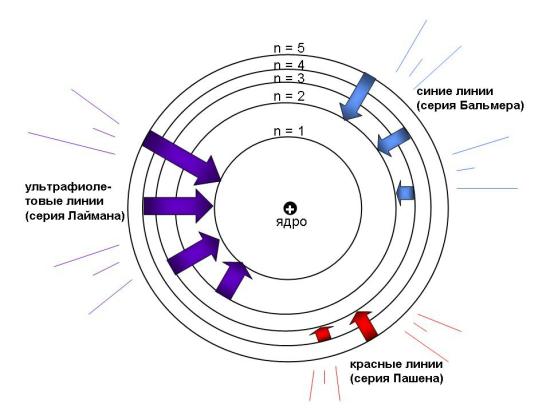
Рис. 2-15. Электронные переходы в атоме водорода: серия Лаймана (самое богатое энергией ультрафиолетовое излучение) возникает в результате переходов с уровней n = 5, 4, 3, 2 в основное состояние (n = 1). Серия Бальмера (видимый свет) возникает при переходах с уровней n = 5, 4, 3 на уровень n = 2. Серия Пашена (красный свет) возникает в результате переходов с уровней n = 6, 5, 4 на уровень n = 3. Серии линий в спектре водорода названы именами открывших их ученых. Происхождение спектральных линий впервые объяснил Н. Бор.
На Солнце кванты света испускаются возбужденными атомами многих элементов, поэтому, как уже говорилось, его спектр кажется нам "непрерывным" (см. рис. 2-11 в начале этого параграфа).
В атоме водорода только один электрон и его спектр испускания относительно прост. В спектрах испускания атомов других элементов число линий больше. Еще до появления модели Бора физики научились различать в таких спектрах близко расположенные линии, отличающиеся по внешнему виду. Одни из них (очень узкие) получили название "резких" (от англ. sharp). Наиболее яркие линии назвали "главными" (от англ. principle). Наблюдались более широкие линии - их назвали "размытыми" (diffuse). Еще один сорт линий имеет название "фундаментальных" (от англ. fundamental). По первым буквам английских названий говорили о наличии в спектрах испускания s-, p-, d- и f-линий. Применительно к модели Бора это означает, что в спектрах атомов более сложных, чем водород, постоянные электронные уровни могут состоять из нескольких близко расположенных подуровней:
s-подуровень назван по "резкой" (sharp) линии,
p-подуровень назван по "главной" (principal) линии,
d-подуровень назван по "диффузной", “размытой” (diffuse) линии,
f-подуровень назван по "фундаментальной" (fundamental) линии.
Сложное устройство уровней показано на рис. 2-6, который мы здесь воспроизводим еще раз:
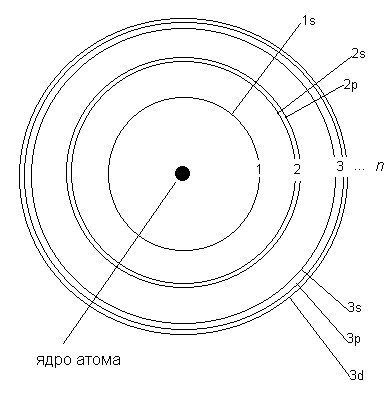
Рис. 2-6. Электронные подуровни атомов более сложных, чем водород. Наличие подуровней объясняет происхождение в спектрах "резких" (sharp), "главных" (principle) и "размытых" (diffuse) линий. Более высокие уровни на рисунке не показаны.
С помощью спектров выяснилось, что первый уровень (n = 1) не содержит каких-либо подуровней, кроме s. Второй уровень состоит из двух подуровней (s и p), 3-й уровень - из трех подуровней (s, p, и d) и т.д. Как мы видим, подуровни обозначаются по первым буквам английских названий соответствующих линий в спектрах. В дальнейшем более высокие подуровни стали обозначать, просто продолжая латинский алфавит: g-подуровень, h-подуровень и т.д.
На рис. 2-16 показана диаграмма части энергетических переходов электронов в атоме лития, полученная из спектра испускания раскаленных паров этого металла.
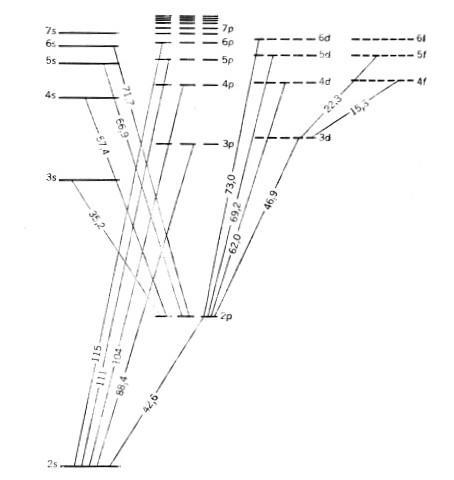
Рис. 2-16. Диаграмма части энергетических уровней и подуровней атома лития. Цифры на линиях показывают относительную энергию тех или иных переходов электрона. Уровень 1s находится намного ниже уровня 2s и не поместился в масштаб рисунка (из книги Дж. Кемпбела "Современная общая химия", М.: Мир, 1975, т. 1, с. 109).
Можно заметить, что на рис. 2-16 некоторые подуровни изображены состоящими из нескольких одинаковых по энергии "полочек". Например, p-подуровни состоят из трех одинаковых по энергии частей, d-подуровни - из пяти, f-подуровни - из семи. Откуда это стало известно? Еще в 1896 году немецкий физик П. Зееман поместил в сильное магнитное поле устройство, аналогичное водородной лампе, но наполненное парами раскаленного натрия. Обнаружилось, что в магнитном поле число линий в спектрах испускания возрастает (эффект Зеемана). Аналогичное явление наблюдается и в сильном электрическом поле. Пока на электроны действуют только внутренние силы ядра, часть из них может находиться в состоянии с одинаковой энергией. Но когда появляется дополнительное, внешнее поле, эта энергия уже не может оставаться одинаковой. Анализ спектров Зеемана значительно позже привел физика-теоретика Вольфганга Паули к мысли о том, что на одной энергетической "полочке" может помещаться не больше двух электронов. А чтобы противостоять мощным силам отталкивания, такие электроны должны обладать разным спином (к этому свойству мы вернемся чуть позже). Получается, что в атоме не может быть двух электронов в одинаковом состоянии. Этот вывод известен как принцип (или запрет) Паули.
Физические эксперименты позволяют определить заселенность электронами уровней и подуровней. Для этого надо измерять энергию ионизации атомов, т.е. энергию отрыва от него электронов. Сначала измерить энергию, необходимую для удаления из атома первого электрона, затем 2-го, 3-го и т.д. Оказалось, что во всех атомах есть электроны, для которых энергии ионизации близки. Например, для аргона (в его электронной оболочке 18 электронов) обнаруживаются пять таких групп с близкими энергиями ионизации. В них 2, 2, 6, 2 и 6 электронов. Но 5 самых нижних энергетических уровней атома соответствуют подуровням 1s, 2s, 2p, 3s и 3p (это известно из спектров испускания). В таком случае s-подуровень должен состоять только из одной орбитали (на ней 2 электрона), p-подуровень - из трех орбиталей (там 6 электронов - по два на каждую орбиталь). Можно показать, что d-подуровень в обычных условиях (без внешнего поля) состоит из пяти орбиталей с одинаковой энергией, а f-подуровень - из семи.
Модель Бора постепенно уточнялась. Ученых она привлекала тем, что с её помощью можно было делать довольно точные расчеты. Например, можно было вычислить энергию атома водорода в основном и возбужденном состояниях, определить его радиус, вычислить энергию ионизации и т.д. Для этих целей модель была снабжена ясным и понятным для многих исследователей математическим аппаратом, который разработали в основном сам Н. Бор и его последователь А. Зоммерфельд. Для проведения расчетов требовалось описывать состояние электрона в атоме, т.е. указывать его точный "адрес" в электронной оболочке (точнее - в модели электронной оболочки) с помощью так называемых квантовых чисел. Мы уже знаем, что каждый электрон существует на каком-либо уровне (1, 2, 3, и т.д.). Этот уровень обозначается числом n, которое получило название главного квантового числа. Понятно, что число n может принимать только целые значения.
Поскольку уровням уже присвоено главное квантовое число n, для подуровней было введено вспомогательное квантовое число l. Если главное квантовое число n - это “адрес” уровня, то число l - “адрес” подуровня:
l = 0 – это s-подуровень,
l = 1 – это p-подуровень,
l = 2 – это d-подуровень,
l = 3 – это f-подуровень,
Давайте попробуем разобраться, почему были выбраны именно такие, а не иные значения l для разных подуровней. Для этого посмотрим на уже знакомую нам орбитальную диаграмму на рис. 2-17.
Рис. 2-17. Квантовые числа n, l, m для описания электронных оболочек атомов.
Значения l тесно связаны с числом орбиталей на каждом подуровне. Например, в значении l = 2 “скрыты” пять орбиталей d-подуровня: -2, -1, 0, +1, +2. Значение l = 1 дает три орбитали p-подуровня: -1, 0, +1. А при l = 0 орбиталь на s-подуровне только одна. Нетрудно вычислить, что в значении l = 3 “зашифрованы” семь орбиталей f-подуровня: -3, -2, -1, 0, +1, +2, +3.
Далее требовалось обозначить "адреса" орбиталей на каждом подуровне. Поскольку орбитали атома становятся "видны" только в магнитном поле, очередное квантовое число, записывающее “адрес” орбитали в атоме, назвали магнитным квантовым числом m. Это квантовое число принимает значения от -l до +l, то есть имеет ровно столько значений, сколько орбиталей существует на каждом подуровне.
Давайте с помощью уже известных нам трех квантовых чисел n, l и m запишем “адрес”, орбитали, которая на рис. 2-17 выделена красным цветом. Потом мы сможем этим же способом записывать “адреса” любых других орбиталей и находящихся на них электронов.
Выделенная орбиталь находится на 3-м уровне: следовательно, ее главное квантовое число n = 3. Эта орбиталь находится на d-подуровне: следовательно, ее вспомогательное квантовое число l = 2. Наконец, для этой орбитали магнитное квантовое число m = -2. Итак, “адрес” выделенной орбитали: n = 3, l = 2, m = -2.
Последнее квантовое число, которое потребовалось для описания электрона в атоме, называется спиновым квантовым числом s. Спин (по английски - веретено), можно представить как вращение заряда электрона вокруг собственной оси - по часовой стрелке и против часовой стрелки. Спиновое квантовое число может принимать, следовательно, только два значения и в квантовой механике они приняты такими: s = +1/2 и s = -1/2. В современной волновой модели строения атома (о ней - в конце этого параграфа) уже затруднительно рассматривать электрон как вращающуюся частицу конечных размеров. Следует признать, что прежняя трактовка спина в значительной мере утратила смысл. Спин связан с движением заряда внутри самого электрона и не зависит от перемещения электрона в трехмерном пространстве. Здесь нам важно понимать, что существует некое фундаментальное различие между электронами (спин электрона), которое позволяет им существовать на одной орбитали в состоянии с одинаковой энергией, несмотря на сильнейшее отталкивание одноименных зарядов этих электронов.
В качестве примера давайте запишем полный набор квантовых чисел для электрона, обведенного красным кружком в орбитальной диаграмме атома азота. Этот электрон характеризуется набором квантовых чисел: n = 2 (находится на 2-м уровне), l = 1(находится на p-подуровне), m = +1 (находится на последней из трех одинаковых p-орбиталей, s = +1/2 (этот электрон заселился первым на данную p-орбиталь).
Заметим, что это справедливо для атома, в котором первым занял место в электронной оболочке на 1s-подуровне электрон со спином +1/2. Но таких атомов в природе ровно половина, а другая половина начинает заселение своей оболочки электроном со спином -1/2. Для простоты дальше мы будем рассматривать только те 50% атомов любых элементов, где самым первым в оболочку попал электрон с s = +1/2.
Можно решать и обратную задачу. Допустим, последним электронную оболочку некоего элемента заселяет электрон с набором квантовых чисел:
n = 3, l = 2, m = -2, s = +1/2.
Какой это элемент? Какова его полная электронная формула? Решение заключается в том, что данный электрон находится на 3-м уровне (n = 3), причем на d-подуровне (l = 2). Полезно нарисовать все пять d-орбиталей и расположить над ними значения магнитного квантового числа m от -2 до +2. У нас это уже сделано на рис. 2-17, причем нужная орбиталь (m = -2) выделена красным цветом. Расположив на ней единственный электрон (стрелка вверх, т.к. s = +1/2) и зная, что он последний, мы приходим к выводу, что остальные d-орбитали пусты. Теперь мы уже можем записать сокращенную электронную формулу элемента: …3d1. Этот элемент легко найти в периодической таблице - это скандий 21Sc. Если вы еще не совсем уверенно обращаетесь с Периодической таблицей, то можно заполнить электронами на рис. 2-17 все нижние уровни и подуровни вплоть до первой 3d-орбитали, поместив на нее единственный d-электрон. Всего на орбитальной диаграмме элемента поместится ровно 21 электрон (проверьте!), следовательно, в его ядре 21 протон и его порядковый номер в таблице Менделеева тоже 21 (Sc). Орбитальная диаграмма помогает записать и полную электронную формулу для скандия: 1s2 2s2 2p6 3s2 3p6 4s2 3d1.
Как мы видим, каждый электрон в атоме имеет свой собственный “адрес”, записанный набором из четырех квантовых чисел. Например, если два электрона находятся на одном и том же уровне (имеют одинаковое число n), и даже на одном подуровне (например, p-подуровне), то они обязательно расположатся на разных орбиталях - то есть будут отличаться числом m. А если орбитали уже полностью заполнены, то два находящиеся на них электрона обязательно должны отличаться друг от друга спиновым квантовым числом s. Таким образом, теперь мы можем дать более строгую формулировку принципа или запрета Паули: