Уравнения прямых и кривых на плоскости

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0.

Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени – это прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:

1. Общее уравнение прямой:

Ax + By + C = 0. (1)

2. Уравнение прямой с угловым коэффициентом:

y - y_o = k (x - x_o), (2)

где k - угловой коэффициент прямой, то есть k = tg a, где a - величина угла, образованного прямой с осью Оx, M (x_o, y_o ) - некоторая точка, принадлежащая прямой.

3. Уравнение прямой в отрезках:

x/a + y/b = 1, (3)

где a и b - величины отрезков, отсекаемых прямой на осях координат.

4. Уравнение прямой, проходящей через две данные точки - A(x₁, y₁) и B(x₂, y₂ ):

. (4)

5. Уравнение прямой, проходящей через данную точку A(x₁, y₁) параллельно данному векторуa(m, n):

. (5)

6. Нормальное уравнение прямой:

rn - р = 0, (6)

где r - радиус-вектор произвольной точки M(x, y) этой прямой,n- единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.

Нормальное уравнение прямой в координатной форме имеет вид:

x cos a + y sin a - р = 0,

где a - величина угла, образованного прямой с осью Оx.

Уравнение пучка прямых с центром в точке А(x₁, y₁) имеет вид:

y-y₁ = l(x-x₁ ),

где l - параметр пучка. Если пучок задается двумя пересекающимися прямыми A₁x +B₁y+ C₁=0, A₂ x + B₂ y + C₂ = 0, то его уравнение имеет вид:

l (A₁ x + B₁ y + C₁) + m (A₂ x + B₂ y + C₂ )=0,

где l и m - параметры пучка, не обращающиеся в 0 одновременно.

Величина угла между прямыми y = kx + b и y = k₁ x + b₁ задается формулой:

tg j = .

Равенство 1 + k₁ k = 0 есть необходимое и достаточное условие перпендикулярности прямых.

Для того чтобы два уравнения

A₁ x + B₁ y + C₁= 0, (7)

A₂ x + B₂ y + C₂ = 0, (8)

задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:

A₁/A₂ = B₁/B₂ = C₁/C_2.

Уравнения (7), (8) задают две различные параллельные прямые, если

A₁/A₂ = B₁/B₂ и B₁/B₂ ¹ C₁/C_2;

прямые пересекаются, если

A₁/A₂ ¹ B₁/B₂.

Расстояние d от точки M_о(x_о, y_о) до прямой есть длина перпендикуляра, проведенного из точки M_о к прямой. Если прямая задана нормальным уравнением, то

d = êr n - р ê,

где r - радиус-вектор точки M_о или, в координатной форме, d = êx_о cosa + y_о sina - р ê.

 

Общее уравнение кривой второго порядка имеет вид:

Ax² + Bxy + Cy² + Dx +Ey +F = 0.

Предполагается, что среди коэффициентов уравнения A, B, C есть отличные от нуля.

Окружностью называется геометрическое место точек, равноудаленных от данной точки (центра).

Нормальное уравнение окружности имеет вид ,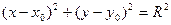

где x₀, y₀ – координаты центра окружности, R – радиус окружности.

После раскрытия скобок в этом уравнении получается общее уравнение окружности

,

где , , .

Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F₁ и F₂ (фокусов) есть величина постоянная, равная 2a, причем , где 2с - расстояние между фокусами.

Каноническое уравнение эллипса имеет вид

,

где 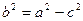, если и фокусы находятся на оси OX.

Параметры a и b называются полуосями эллипса.

Отношение 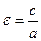называется эксцентриситетом эллипса. Он характеризует форму эллипса. Очевидно, что 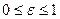, причем для окружности .

Расстояние от любой точки эллипса М(x, y) до его фокусов (фокальные радиусы) находятся по формулам

, .