Розв'язання.

.

 

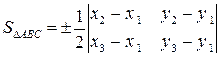ІІ. Рівняння лінії на площині

Нехай на площині задано декартову систему координат хОу і зада­но деяку лінію L. Будь-яка лінія — це геометричне місце точок, що мають деяку загальну властивість. Аналітичний вираз цієї властивості, як зв'язок між координатами х,у точок, що лежать на лінії L, представ­ляє рівняння з двома змінними х, у, загальний вигляд якого F(x,y) = 0.

Означення. Рівняння F(x, y) = 0 називається рівнянням лінії L (при заданій системі координат), якщо його задовольняють координати х, у будь-якої точки, що лежить на L, і не задовольняють координати точок, що не лежать на L. Говорять також, що рівняння F(x, y) = 0 визначає лінію L.

Будь-яку лінію L на площині можна представити рівнянням F(x, у) = 0, що виражає загальну властивість точок тільки цієї лінії і яке задовольняють координати тих і лише тих точок, що належать цій лінії.

Таким чином, виникають дві задачі.

1. По заданому рівнянню F(x, y) = 0 визначити вигляд лінії L та її властивості.

2.Скласти рівняння лінії L за заданою загальною властивістю всіх точок цієї лінії.