КОНВЕКТИВНЫЙ ТЕПЛООБМЕН (ТЕПЛООТДАЧА)

В принципе количество переданной теплоты можно описать уравнением Фурье, однако на практике это невозможно. Большие сложности возникают при определении температурного градиента у стенки, а также его изменение по поверхности теплообмена. Поэтому в основу расчётов положена более простая формула Ньютона (1643— 1717) и Рихмана (1711-1753гг.), согласно которой тепло­вой поток в процессе теплоотдачи про­порционален площади поверхности теп­лообмена F и разности температур по­верхности t_c и жидкости t_ж:

Q = aF(t_c-t_ж). (9.1)

В процессе теплоотдачи независимо от направления теплового потока Q (от стенки к жидкости или наоборот) значе­ние его принято считать положительным, поэтому разность t_c — t_ж. берут по абсо­лютной величине.

Коэффициент пропорциональности а называется коэффициентом теп­лоотдачи; его единица измерения Вт/(м²-К). Он характеризует интенсив­ность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жид­кости в 1 К.

Коэффициент теплоотдачи обычно определяют экспериментально, измеряя тепловой поток Q и разность температур Δt = t_c — t_жв процессе теплоотдачи от поверхности известной площади F. Затем по формуле (9.1) рассчитывают а. При проектировании аппаратов (проведении тепловых расчетов) по этой формуле оп­ределяют одно из значений Q, F или Δt. При этом а находят по результатам обобщения ранее проведенных экспери­ментов.

Строго говоря, выражение (9.1) справедливо лишь для дифференциально малого участка поверхности dF, т. е.

δQ = adF\t_c-t_ж), (9.2)

поскольку коэффициент теплоотдачи мо­жет быть не одинаковым в разных точках поверхности тела.

Для расчета полного потока теплоты от всей поверхности нужно проинтегри­ровать обе части уравнения (9.2) по по­верхности

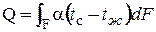(9.3)

Обычно температура поверхности и средняя температура жидкости по­стоянны, тогда

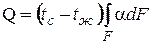(9.4)

В расчетах используются понятия сред­него по поверхности коэффициента теп­лоотдачи:

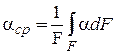. (9.5)

Рис. 9.1. Распределение скоростей и темпера­тур теплоносителя около вертикальной теплоотдающей поверхности при естественной кон­векции

В окончательном виде формула Ньютона используется в виде (9.1),где коэффициент теплоотдачи α = α_ср . Коэффициент теплоотдачи а зависит от физических свойств жидкости и ха­рактера ее движения. Различают естественное и вынужденное движение жидкости. В этих случаях говорят о свободной (естественной) и вынужденной конвекции. Вынужденное движение создается внеш­ним источником (насосом, вентилятором, ветром). Естественная конвекция возни­кает за счет теплового расширения жид­кости, нагретой около теплоотдающей поверхности (рис. 9.1) в самом процессе теплообмена. Она будет тем сильнее, чем больше разность температур Δt = t_c — t_жи температурный коэффициент объемно­го расширения:

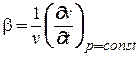(9.7)

где v = 1/ρ — удельный объем жидкости.

Для газов, которые в большинстве случаев приближенно можно считать идеальными, коэффициент объемного расширения можно получить, воспользо­вавшись уравнением Клапейрона:

β=1/Т (9.8)

Температурный коэффициент объем­ного расширения капельных жидкостей значительно меньше, чем газов.

Разность плотностей жидкостей приводит к тому, что на любой единичный объем прогретой жид­кости будет действовать подъемная сила F_n, равная алгебраической сумме вытал­кивающей архимедовой силы и силы тяжести.

Подъемная сила F_n перемещает про­гретую жидкость вверх без каких-либо побуждающих устройств (возникает естественная конвекция). Все рассужде­ния о возникновении естественной кон­векции справедливы и для случая охлаж­дения жидкости с той лишь разницей, что жидкость около холодной поверхно­сти будет двигаться вниз, поскольку ее плотность будет больше, чем вдали от поверхности.

Из-за вязкого трения течение жидко­сти около поверхности затормаживается, поэтому, несмотря на то что наибольший прогрев жидкости, а соответственно и подъемная сила при естественной кон­векции будут около теплоотдающей по­верхности, скорость движения частиц жидкости, прилипших к самой поверхно­сти, равна нулю (см. рис. 9.1).

Сила вязкого трения зависит от вязкости жидкости, характеризуемой коэффициентом ди­намической вязкости жидкости μ, измеряемой в Н∙с/м² (или Па∙с) и кинематической вяз­кости ν = μ /ρ (м²/с). Оба эти коэффициента характеризуют физические свойства жидкости, их значения приводятся в справочниках [15].

ПОГРАНИЧНЫЙ СЛОЙ

Рассмотрим процесс теплоотдачи от потока теплоносителя к продольно - омы­ваемой им пластине. Скорость и темпера­тура набегающего потока постоянны и равны w_ж и t_ж (рис. 9.2).

Рис. 9.2. Образование пограничного слоя (а) и распределение местного (локального) коэф­фициента теплоотдачи (б) при продольном об­текании тонкой пластины

Как уже отмечалось, частицы жидко­сти, непосредственно соприкасающиеся с поверхностью, адсорбируются («при­липают») к ней. Соприкасаясь с непод­вижным слоем, тормозятся и более уда­ленные от поверхности слои жидкости. Зона потока, в которой наблюдается уменьшение скорости (w < w_ж), вызван­ное вязким взаимодействием жидкости с поверхностью, называется гидроди­намическим пограничным слоем. За пределами пограничного слоя те­чет невозмущенный поток. Четкой грани­цы между ними нет, так как скорость wпо мере удаления от поверхности по­степенно (асимптотически) возрастает до w_ж. Практически за толщину гидроди­намического пограничного слоя условно принимают расстояние от поверхности до точки, в которой скорость wотличается от скорости невозмущенного потока w_ж незначительно (обычно на 1 %).

На начальном участке (при малых значениях х гидродинамический слой очень тонок (в лобовой точке с координа­той х = 0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешива­ясь. При удалении от лобовой точки тол­щина пограничного слоя растет. На не­котором расстоянии х = х_кр ламинарное течение становится неустойчивым. В по­граничном слое появляются вихри (тур­булентные пульсации скорости). Посте­пенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины в турбулентном пограничном слое сохра­няется тонкий ламинарный, или вязкий подслой, где скорость не­велика и силы вязкости гасят турбулент­ные вихри.

Аналогичным образом осуществляет­ся и тепловое взаимодействие потока с пластиной. Частицы жидкости, «при­липшие» к поверхности, имеют темпера­туру, равную температуре поверхности t_c. Соприкасающиеся с этими частицами движущиеся слои жидкости охлаждают­ся, отдавая им свою теплоту. От сопри­косновения с этими слоями охлаждаются следующие более удаленные от повер­хности слои потока — так формируется тепловой пограничный слой, в пределах которого температура меня­ется от t_c на поверхности до t_x в невоз­мущенном потоке. По аналогии с гидро­динамическим пограничным слоем тол­щина теплового пограничного слоя δ_т принимается равной расстоянию от по­верхности до точки, в которой избыточ­ная температура жидкости θ = t — t_c от­личается от избыточной температуры не­возмущенного потока θ_ж = t_ж — t_c на ма­лую величину (обычно на 1 %).

С удалением от лобовой точки коли­чество охлаждающейся у пластины жид­кости увеличивается, и толщина теплово­го пограничного слоя возрастает анало­гично возрастанию δ_т . В общем случае толщины теплового и гидродинамическо­го слоев не равны, но часто достаточно близки друг к другу, особенно в газах.

При ламинарном течении тепловой поток от охлаждающейся в пограничном слое жидкости переносится к поверхно­сти пластины только за счет теплопроводности. При этом плотность теплового потока по толщине пограничного слоя неодинакова: на внешней границе q = 0, ибо дальше жидкость не охлаждается; по мере приближения к поверхности зна­чение q возрастает. Для качественного анализа можно предположить, что плот­ность теплового потока q по всей толщи­не пограничного слоя такая же, как и у поверхности. Это условие соответ­ствует задаче о переносе теплоты тепло­проводностью через плоскую стенку (по­граничный слой толщиной δ_т с темпера­турами t_c и t_ж на поверхностях). Со­гласно решению (8.9) Q ~ λF (t_c — t_x)/ δ_т . Сравнивая это выражение с формулой (9.1), получим для ка­чественных оценок коэффициент теплоотдачи

a ~ λ/ δ_т . (9.11)

В переходном, а тем более турбулент­ном режимах основное термическое со­противление сосредоточено в тонком ла­минарном подслое, поэтому формула (9.11) приближенно пригодна для оце­нок и в этих режимах, если вместо δ_т под­ставлять толщину ламинарного подслоя.

С увеличением толщины теплового пограничного слоя при ламинарном тече­нии жидкости у поверхности пластины интенсивность теплоотдачи уменьшается. В переходной зоне общая толщина по­граничного слоя продолжает возрастать, однако значение а при этом увеличивает­ся, потому что толщина ламинарного подслоя убывает, а в образующемся тур­булентном слое тепло переносится не только теплопроводностью, но и конвек­цией вместе с перемещающейся массой, т. е. более интенсивно. В результате сум­марное термическое сопротивление теп­лоотдачи убывает.

После стабилизации толщины лами­нарного подслоя в зоне развитого тур­булентного режима коэффициент тепло­отдачи вновь начинает убывать из-за возрастания общей толщины погранич­ного слоя.

Из формулы (9.11) видно, что ко­эффициент теплоотдачи к газам, облада­ющим малой теплопроводностью, будет ниже, чем коэффициент теплоотдачи к капельным жидкостям, а тем более к жидким металлам.

Рис. 9.3. Схема термообработки листовых из­делий на «воздушной подушке»

Для получения высоких коэффициен­тов теплоотдачи к газам стараются ка­ким-либо способом уменьшить толщину пограничного слоя. Проще всего для это­го увеличить скорость течения газа. Ин­тенсификация теплоотдачи происходит и при резкой искусственной турбулизации пограничного слоя струями, направ­ленными по нормали к поверхности (рис. 9.3). С помощью системы из мно­жества струй можно обеспечить высокие значения а от достаточно протяженной поверхности. Так, в воздушных струях с относительно невысокими скоростями истечения (w ~ 60 м/с) удается дости­гать значений а = 200 - 300 Вт/(м²-К). При обычном продоль­ном обтекании протяженных поверхно­стей толщина пограничного слоя на них велика, а коэффициенты теплоотдачи к воздуху при таких скоростях обычно ниже 100 Вт/(м²-К).

Использование системы струй в ряде случаев позволяет не только улучшить теплообмен, но и удачно организовать технологический процесс. Направленные вверх струи могут удерживать листовое изделие на «воздушной подушке». Это облегчает транспортировку изделия, уменьшает механические нагрузки на не­го и практически исключает повреждение поверхности. Последнее немаловажно, например, при термообработке листового стекла.

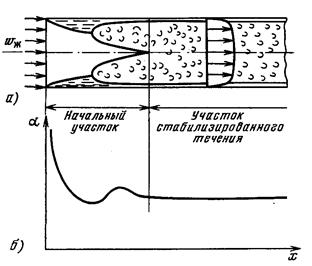
При течении жидкости в трубе тол­щина пограничного слоя вначале растет симметрично по всему периметру, как на пластине (рис. 9.4, а), до тех пор, пока слои с противоположных стенок не со­льются на оси трубы. Дальше движение стабилизируется и фактически гидроди­намический (аналогично и тепловой) по­граничный слой заполняет все сечение трубы. В зависимости от конкретных ус­ловий пограничный слой на начальном

участке может успеть перейти в турбу­лентный, а может и не успеть. Соответ­ственно стабилизированный режим течения в трубе будет либо турбулентным с ламинарным подслоем около стенки, либо ламинарным по всему сечению.

Рис. 9.4. Образование пограничного слоя (а) и распределение местного коэффициента теп­лоотдачи (б) при турбулентном течении тепло­носителя внутри трубы

В связи с особенностями течения жидкости в трубе изменяется и само по­нятие коэффициента теплоотдачи. Для пластины коэффициент а рассчитывался как отношение плотности теплового по­тока q к разности температур внешнего невозмущенного потока и поверхности (или наоборот при t_c > t_ж). В трубе по­граничный слой занимает все сечение и невозмущенного потока нет, поэтому под коэффициентом теплоотдачи в трубе понима­ют отношение плотности теплового по­тока q к разности температуры стенки и среднемассовой температуры жидко­сти, протекающей через данное сечение трубы. Экспериментально среднемассовая температура жидкости определяется измерением ее температуры после хоро­шего перемешивания.

Локальный коэффициент теплоотда­чи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 9.4, б), а на участке стабилизиро­ванного течения а_ст = const, поскольку толщина пограничного слоя (δ_т = r) по­стоянна. С увеличением скорости тече­ния теплоносителя в трубе а_ст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растет тол­щина всего пограничного слоя δ_т = r.

Чтобы получить аналитическое выра­жение для коэффициента теплоотдачи, необходимо интегрировать систему диф­ференциальных уравнений, описываю­щих движение жидкости и перенос теплоты в ней. Даже при существенных упрощениях это возможно лишь в от­дельных случаях при ламинарном тече­нии жидкости, поэтому обычно для полу­чения расчетных зависимостей прибега­ют к экспериментальному изучению яв­ления.

ПОНЯТИЕ О МЕТОДЕ АНАЛИЗА РАЗМЕРНОСТЕЙ И ТЕОРИИ ПОДОБИЯ

Основная трудность, возникающая при экспериментальном исследовании конвективного теплообмена, заключается в том, что коэффициент теплоотдачи за­висит от многих параметров. Например, средний по поверхности коэффициент теплоотдачи от продольно омываемой пластины (см. рис. 9.2) зависит от длины пластины l, скорости набегающего по­тока w_ж и теплофизических параметров жидкости:

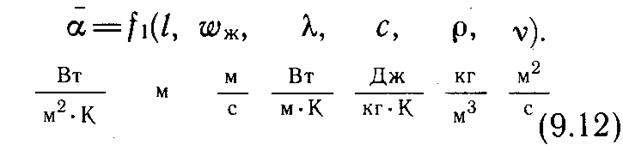
Если проводить эксперименты, изме­няя т раз каждый из шести параметров, влияющих на теплообмен, то суммарное число экспериментов будет N = m⁶, т. е. порядка 10⁶.

Теория показывает, что число пара­метров зависит от выбора единиц изме­рения. Наименьшее число параметров получится, если единицы измерения бу­дут связаны с самой решаемой задачей. Так, в качестве единицы длины можно принять не метр, а длину пластины l. Для перевода всех параметров в «но­вую» систему единиц измерения поделим их на l в той же степени, в которой длина входит в их размерность:

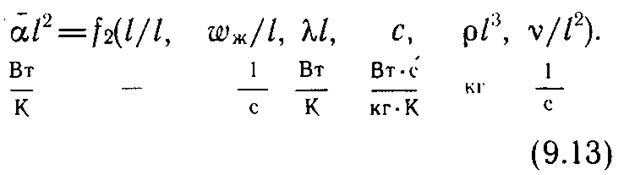
Число параметров в правой части уравнения уменьшилось, так как l/l==1, т. е. мы избавились от того параметра, который приняли за единицу измерения. Если теперь ввести еще три «новых» еди­ницы измерения: для времени l ²/v, для массы рl ³ и, наконец, для отношения тепловой мощности к перепаду темпера­тур λl (в рассматриваемой системе вели­чин единицы Вт и К раздельно не встре­чаются, а входят лишь в комбинации Вт/К), то в правой части рассматривае­мой зависимости останется всего два безразмерных параметра:

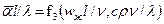. (9.14)

Такие же безразмерные параметры получаются и при анализе теплоотдачи от поверхности трубы, но определяющим размером в них будет не длина l, а диа­метр d, соответственно внутренней — при течении жидкости внутри трубы и наружный — при наружном обтекании одной трубы или пучка труб.

Согласно теории подобия зави­симость между размерными величина­ми, определяющими данный процесс, мо­жет быть представлена в виде зависимо­сти между составленными из них безразмерными величинами, называемыми критериями подобия. В данном случае число таких критериев подобия равно 3.

Каждый из безразмерных критериев имеет определенный физический смысл. Их принято обозначать первыми буквами фамилий ученых, внесших су­щественный вклад в изучение процессов теплопереноса и гидродинамики, и на­зывать в честь этих ученых.

Число Нуссельта (1887—1957 гг.):

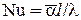(9.15)

представляет собой безразмерный коэф­фициент теплоотдачи.

Число Рейнольдса (1842—1912):

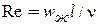(9.1)

выражает отношение сил инерции (скоростного напора) к силам вязкого трения.

При малых числах Re преобладают силы вязкости и режим течения жидкости ламинарной (отдельные струи потока не перемешиваются, двигаясь параллельно друг другу, и всякие случайные завихрения быстро затухают под действием сил вязкости). При турбулентном течении в потоке преобладают силы инерции, поэтому завихрения интенсивно развиваются. При продольном обтекании пластины (см. рис. 9.2) ламинарное течение в пограничном слое нарушается на расстоянии х_кр от лобовой точки, на кото­ром Re_кр ≈ 5-10⁵.

При течении жидкостей в трубах (см. рис. 9.4) ламинарный режим на ста­билизированном участке наблюдается до Re_кр = 2300, а при Re>10⁴ уста­навливается развитый турбулентный ре­жим (здесь линейный размер d — внутренний диаметр трубы).

Число Прандтля (1875—1953):

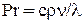(9.17)

состоит из величин, характеризующих теплофизические свойства вещества и по существу само является теплофизической константой вещества. Значение чис­ла Рr приводится в справочниках [15].

В случае естественной конвекции скорость жидкости вдали от поверхности w_ж = 0 и соответственно Re = 0, но на теплоотдачу будет влиять подъемная сила F_п. Это приведет к появлению друго­го безразмерного параметра — числа Грасгофа:

Gr=gβl ³Δt/v_ж². (9.18)

Оно характеризует отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.

При исследовании локального тепло­обмена кроме безразмерных чисел в уравнения войдут безразмерные коор­динаты, представляющие собой отноше­ние обычных координат к определяюще­му размеру. Для продольно омываемой пластины это будет Х = х/l.

на основании результатов экспериментов, а затем по­добрать вид функции. Не исключено, что в данном случае мы бы угадали лога­рифмическую зависимость, но при не­большом интервале изменения парамет­ров ее легко спутать с линейной, тем более что экспериментальные точки сами отклоняются от точной кривой из-за по­грешности измерений. Никогда нет пол­ной уверенности, что подобранная эмпи­рическая зависимость точно соответству­ет неизвестному реальному закону, по­этому область ее применения всегда ограничивается теми интервалами изме­нения безразмерных параметров, в кото­рых проведен эксперимент.