Гипербола
гиперболойназывается линия, для каждой точки  на которой абсолютная величина разности расстояний до двух заданных точек
на которой абсолютная величина разности расстояний до двух заданных точек  и
и  этой же плоскости (фокусов эллипса) есть величина постоянная, меньшая, чем расстояние между фокусами:
этой же плоскости (фокусов эллипса) есть величина постоянная, меньшая, чем расстояние между фокусами:  .
.
§ Каноническое уравнение гиперболы с центром в начале координат:
 .
.
где 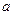 — действительная,
— действительная,  — мнимая полуось гиперболы. Числа
— мнимая полуось гиперболы. Числа  и
и  — соответственно действительная и мнимая оси гиперболы.
— соответственно действительная и мнимая оси гиперболы.
Признак уравнения гиперболы: коэффициент  при
при  и коэффициент
и коэффициент  при
при 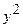 имеют разные знаки и по абсолютной величине не равны между собой.
имеют разные знаки и по абсолютной величине не равны между собой.
Для гиперболы  :
:
1) координаты фокусов:  ,
,  , где
, где  — половина расстояния между фокусами (см. рис);
— половина расстояния между фокусами (см. рис);
2) числа 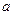 ,
,  и
и  связаны соотношением
связаны соотношением  ;
;
3) расстояние между фокусами равно  ;
;
4) точки  и
и  называются вершинами гиперболы, точка
называются вершинами гиперболы, точка  - центром гиперболы;
- центром гиперболы;

Прямоугольник, центр которого совпадает с точкой  , а стороны равны и параллельны осям гиперболы, называется основным прямоугольником гиперболы.
, а стороны равны и параллельны осям гиперболы, называется основным прямоугольником гиперболы.
Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы; они определяются уравнениями  .
.
Уравнение  или
или  также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси
также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси  длины
длины  .
.
Пример. Составьте уравнение гиперболы, если её фокусы лежат на оси  и расстояние между ними равно 10, а длина мнимой оси равна 8.
и расстояние между ними равно 10, а длина мнимой оси равна 8.
По условию,  ;
;  . Тогда по формуле
. Тогда по формуле  получим:
получим:
 .
.
Тогда уравнение гиперболы:  .
.
Уравнения  ,
, 
также задают гиперболу, координаты центра которой задаются точкой  .
.
Уравнение гиперболы со смещенным центром в точке  :
:

В школьном курсе математики изучались гиперболы вида  (или
(или  ) как график обратной пропорциональной зависимости.
) как график обратной пропорциональной зависимости.
Положение такой гиперболы зависит от знака и величины  .
.








Асимптотами гиперболы  являются прямые, проходящие через центр гиперболы:
являются прямые, проходящие через центр гиперболы:  .
.
Уравнение гиперболы с центром в точке с координатами  имеет вид
имеет вид

Пример. Построить гиперболу по уравнению 
Приведем данное уравнение к виду  , получим:
, получим:  , значит,
, значит,  ,
,  ,
,  . Точка
. Точка  – центр гиперболы. Ветви находятся в первой и третьей четвертях.
– центр гиперболы. Ветви находятся в первой и третьей четвертях.
Найдем точки пересечения гиперболы с осями координат:
1) с осью  :
: 
2) с осью  :
: 