Основание позиционной системы счисления – это количество различных знаков или символов, которые используются для изображения цифр в данной системе счисления.

 

Основание системы счисления

Цифры, используемые в системе счисления 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F

 

В принципе основанием системы счисления может быть любое натуральное число – два, три, четыре. Следовательно, возможно бесчисленное множество позиционных систем счисления: двоичная, троичная, четверичная и т.д.

Закономерность построения позиционных чисел имеет математическое представление.

Введем обозначения:

q – основание системы счисления;

a_i – любая цифра из множества цифр, принятых в данной системе счисления;

a_i удовлетворяет неравенству

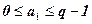
и принимает в этом диапазоне только целые значения;

i – индекс, который обозначает номер разряда, занимаемого цифрой в числе.

 

Позицию для целых чисел обозначим номерами 1,2,…, n, а позиции в правильных дробях – номерами -1, -2,…, -m.

Тогда любое число А в произвольной позиционной системе счисления с основанием q можно записать следующим образом:

A_n = a_n-1q ^n-1 + a_n-2 q ^n-2 + … + a₁q ¹ + a₀q ⁰ + a _-1q ^-1 + … + a _{– m}q ^-m , (1)

 

где qⁱ называется позиционным значением или весом i – го разряда.

Для десятичной системы счисления понятие веса разряда соответствует названиям позиций – единицы, десятки, сотни, десятые доли, сотые доли и т.д.

 

ПРИМЕР: