Порядок выполнения работы.

Лабораторная работа №3

ОБРАБОТКА РЕЗУЛЬТАТОВ СОВОКУПНЫХ ИЗМЕРЕНИЙ

 

Задачи, решаемые при выполнении лабораторной работы

1.1. Составление системы условных уравнений.

1.2. Введение новых переменных с целью упрощения расчетов.

1.3. Вычисление коэффициентов системы нормальных уравнений.

1.4. Определение искомых величин.

1.5. Оценивание характеристик погрешностей измеряемых величин и построение доверительных интервалов.

 

Порядок выполнения работы.

В качестве результатов совокупных измерений использованы измерения углов, полученные на геодезической практике.

2.1. На местности из точки "0" проведены четыре прямые и измерены углы:

ÐАОВ=Х=48° 17¢ 1,4²;

ÐАОС=Y=96° 52¢ 16,8²;

ÐАОД= Z =152° 54¢ 6,8²;

ÐВОС=Y-Х=48° 35¢ 14,3²;

ÐВОД= Z-Х=104° 37¢ 7,8²;

ÐСОД=Z-Y=56° 1¢ 48,9².

 

В вышеприведенную условную систему уравнений входят три неизвестных: Х, Y, Z.

2.1.1. Для упрощения расчетов следует выполнить замену переменных:

Х-48° 17¢ 1,4²=Х¢;

Y-96° 52¢ 16,8²=Y¢;

Z-152° 54¢ 6,8²= Z¢.

2.2. Составить систему условных уравнений и перейти к системе нормальных уравнений. Для составления нормальной системы уравнений определяем коэффициенты этих уравнений, используя таблицу 3.1.

 

Таблица 3.1.

а b С l aa аb ac bb bc сс al bl cl
                         
                         
                         
                         

 

2.3. Вычислить оценки измеряемых величин: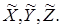

Вычислить остаточные погрешности (невязки )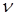

 

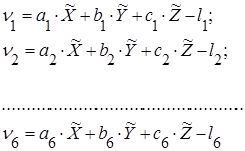
2.4. Вычислить среднее квадратическое отклонение условных уравнений S.

2.5. Вычислить средние квадратические отклонения искомых величин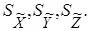

2.6. Построить доверительные интервалы для истинного значения измеряемых величин, используя коэффициенты Стьюдента (см. Приложение 2). Число степеней свободы при этом для всех измеряемых величин равно (n-m),

где n - число уравнений в условной системе;

m - число искомых величин.

3. Изложенный метод обработки совокупных измерений является классическим методом наименьших квадратов. Основные ограничения использования этого метода состоит в предположении, что случайные погрешности свойственны преимущественно свободным членам li.

3.1. Точность результатов совокупных измерений зависит от соотношения числа искомых величин и числа уравнений в условной системе. Чем больше условных уравнений в системе по сравнению с числом искомых величин, тем точнее полученный результат. Если число условных уравнений в системе невелико или оно мало отличается от числа неизвестных, то погрешности определяются с грубым приближением.

3.2. Точность применяемого метода в значительной мере зависит от точности знания функциональных зависимостей условных уравнений системы. Приближенность функциональных зависимостей резко искажает результаты. Если уравнения представляют собой грубые эмпирические формулы, то применение способа наименьших квадратов не дает хороших результатов даже при самых высококачественных экспериментальных данных.

3.3. Изложенный метод может быть использован для экспериментального нахождения градуировочной характеристики средств измерений, измерительных преобразователей. Измеряя на входе величины Х, на выходе – Y, определяют коэффициенты 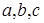и т.д.

3.4. Поскольку решение системы условных уравнений нелинейного вида связано с непреодолимыми трудностями, нелинейные уравнения приводят к линейному виду. Один из методов преобразования нелинейных уравнений в линейные состоит в замене неизвестных так, чтобы условные уравнения системы были линейные. Другой метод заключается в разложении нелинейной функции в ряд Тейлора с сохранением линейной части ряда.