I. Переход от исходного распределения к условному

I. Цель работы

Найти оценки параметров случайной величины Y по данным выборочной совокупности (статистической совокупности). В предположении, что закон распределения случайной величины Y – нормальный, построить кривую распределения. Проверить гипотезу нормальности распределения по критерию Пирсона.

2 Пояснения к работе

Для исследования случайной величины Y проведено n независимых испытаний, в результате которых получена выборочная, или статистическая совокупность (выборка) объёма n. Значения элементов выборки представляют собой последовательность

x₁; x₂; x₃; …, x_n, (I)

среди членов которой могут быть и повторяющиеся. Работу можно разделить на три этапа.

I. Переход от исходного распределения к условному

Если объём статистической совокупности n ³ 40, то все множества значений (I) разбивается на классы. Число классов k определяется по объёму выборки n с помощью таблицы I.

Таблица I

Объём выборки n	40 – 60	60 – 100	100 – 200	200 – 500
Число классов k	6 – 7	7 – 10	10 – 14	14 – 17

Из множества значений, составляющих выборку (I), выбирают наибольшее x_max и наименьшее x_min значения и определяют длину классового промежутка D:

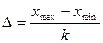(2)

Значение D берется приближенно с той же точностью, с которой определены значения элементов выборки (I), причем так, чтобы последняя цифра значения величины D была четной. Приведенное округление не сказывается на основном результате. Поэтому фактическое число классов может несколько отличаться от выбранного. Чтобы фактическое число классов соответствовало табл. I , рекомендуется при первоначальном выборе k не брать крайних значений, приведенных в столбцах табл. I.

Границы классовых промежутков определяются следующим образом: левая граница первого промежутка принимается равной 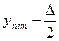. Левая граница каждого следующего промежутка получается прибавлением D к левой границы предыдущего промежутка. Правый конец каждого промежутка меньше левого конца следующего промежутка на единицу последнего десятичного разряда значений в совокупности (I). Границы промежутков вносятся в стб. I. табл. 2.

Таблица 2

Границы промежутков. от до	Середины проме-жутков x_i	Частоты (штрихи)	Частоты Z	Условные значения a	aZ	a²Z	a³Z	a⁴Z

		## ## //
Сумма	SZ	-	SaZ	Sa²Z	Sa³Z	Sa⁴Z

После того как заполнен стб. I табл. 2, переходят к заполнению стб.2. Для каждого элемента выборки (I) находят классовый промежуток, которому принадлежит этот элемент, и в строке этого промежутка в стб.2 ставят штрих. Рекомендуется четыре штриха ставить вертикально, а пятый – горизонтально, перечеркивая им четыре предыдущих. Когда все n штрихов расставлены, подсчитывается их сумма всех частот SZ и записывается в последней строке в табл.2. Все элементы выборки (I), принадлежащие одному и тому же классовому промежутку, считаются равными между собой и равными середине этого промежутка. Середина промежутка определяется как среднее арифметическое его границ и записывается в стб.2. Отметим, что достаточно найти середину только одного из классовых промежутков, так как середины соседних промежутков отличаются друг от друга на D.

Теперь вместо исходной выборки (I) изучается ее приближение, выборочный ряд 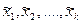, а соответствующие частоты в стб.4 табл.2. Для удобства дальнейших вычислений вводятся условные значения a_i:

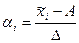(3)

где a_i - i – е условное значение:

x_i – середина i- го классового промежутка;

А – условный нуль.

Условный нуль А – это значение x_i, соответствующее среднему классовому промежутку, а если таковых два, то тому из них, который имеет большую частоту z_i . Заметим, что вычислений по формуле (3) можно не проводить, так как строке табл.2, соответствующей условному нулю А, соответствует a_i = 0, строки над этой имеют соответственно a_i_-1 = -1, a_i_-2 = -2, и т.д., а строки под i-й-a_i₊₁ = 1, a_i₊₂ = 2, a_i₊₃ = 3 и т.д. После этого заполняются стб.6,7,8 и 9, а затем последняя строка – «Сумма» – для этих столбцов.

Пример. Исследовать случайную величину X – прочность (разрывная нагрузка)!!!!, в Н пряжи Т = 18,5 текс !!!(№154) с помощью выборки объема n = 40.

144, 149, 199, 174, 176, 183, 239, 208,

120, 150, 203, 160, 180, 207, 221, 220,

117, 158, 170, 282, 177, 218, 210, 190,

225, 149, 250, 101, 179, 236, 198, 193,

230, 240, 163, 238, 178, 183, 213, 211,

Находим x_min = 101; x_max = 282. Для n = 40 из табл.1 выбираем k = 6. Тогда длина классового промежутка

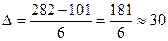
Составляем табл.2 по форме табл.2.

Таблица 3

					m₁	m₂	m₃	m₄
y	x_i		z_i	a_i	a_iZ_i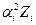
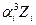
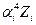
86 – 115 116 – 145 146 – 175 176 – 205 206 – 235 236 – 265 266 – 295	100,5 130,5 160,5 190,5 220,5 250,5 280,5	/ /// ## /// ## ## // ## ## ## /		-3 -2 -1	-3 -6 -8		-27 -24 -8
Сумма

Левая граница I-го интервала