Чётные числа в двоичной системе всегда оканчиваются на 0, а нечётные – на 1.

Например:

6210=1111102

5310=1101012

 

7. Числа вида 2k записываются в двоичной системе как единица и k нулей.

Например:

12810=27=100000002

 

8. Числа вида 2k-1 записываются в двоичной системе как k единиц.

Например:

25510=256-1=28-1=111111112

 

9. Если известна двоичная запись числа N, то двоичную запись числа 2*N можно получить, приписав в конец 0 (нуль).

Например: 710=1112 ; 2*710=1410=11102; 2*1410=2810=111002

 

Отрицательные числа в ЭВМ представляются в обратном и дополнительном кодах.

При выполнении арифметических операций в ЭВМ применяют специальные коды для представления чисел: прямой, обратный и дополнительный коды чисел.

Прямой код двоичного числа – это само двоичное число.

Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 – на 0).

Пример: Дано число X=-1011. Перевести число в обратный код. Хобр=1.0100

Дополнительный код положительного числа совпадает с прямым, а код отрицательного числа образуется как результат увеличения на 1 его обратного кода.

Пример: Дано число X=-1011. Перевести в дополнительный код. Хдоп=1.0101

 

Варианты заданий с решением

1. Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 101010102 2) 101111002 3) 101000112 4) 101011002

Решение: При переводе a и b в двоичное представление, получим: a=AA16 =101010102 , b=2558 =101011012 . Отсюда следует, что подходит значение 101011002,

Ответ: 4

2. Чему равна сумма чисел 718 и 1F16?

1) 778 2) 1111112 3) BB16 4) 8810

Решение: Надо представить числа в двоичном виде и поразрядно сложить:

718=1110012 каждая цифра в 8-ой системе представляется 3-мя битами, 1F16=111112 каждая цифра в 16-ой системе представляется 4-мя битами. (Представление 8-х и 16-х чисел в двоичном виде надо знать!)

+ 11111

____________

 

Полученное двоичное число представим в 8-м и 16-м виде: 10110002=5816=1308 =8810.

Ответ: 4

 

3. Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г используется посимвольное кодирование: А-0, Б-11, В-100, Г-011. Через канал связи передается сообщение: ГБАВАВГ. Закодируйте сообщение данным кодом. Полученную двоичную последовательность переведите в восьмеричный код.

1) DBACACD 2) 75043 3) 7A23 4) 3304043

Решение: Заменяя в сообщении буквы на соответствующий код, получим следующую последовательность:

0111101000100011. Разобьем эту последовательность на триады справа налево: 111 101 000 100 011, представив каждую триаду в виде 8-го числа, получим: 75043

Ответ: 2

 

4. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?

Решение: Для решения задачи достаточно рассмотреть следующие числа в троичной системе счисления: 223, 1223, 2223 и перевести их в десятичную систему счисления:

223=2*3+2=810

1223=1*32+2*3+2=1710

2223=1*32+2*3+2=2610

Ответ: 8, 17, 26

 

5. Сколько единиц в двоичной записи десятичного числа 513?

1) 5 2) 2 3) 3 4) 4

Решение: 513=512+1 => 512=29 = 10000000002 => 513= 10000000002 +1=10000000012

Ответ: 2

 

6. Сколько значащих нулей в двоичной записи числа 254?

1) 1 2) 2 3) 4 4) 8

Решение: 254=255 - 1 => 255=28-1=111111112 – 1=111111102

Ответ: 1

7. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-78)?

1) 3 2) 4 3) 5 4) 6

Решение:

1) переводим число 78 в двоичную систему счисления:

78 = 64 + 8 + 4 + 2 = 26 + 23 + 22 + 21 = 10011102

2) по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов, причем старший разряд - знаковый

3) в прямом коде число будет представлено в виде:

110011102

4) делаем инверсию битов (заменяем везде, кроме знакового разряда, 0 на 1 и 1 на 0) и получим число в обратном коде:

110011102 → 101100012

5) добавляем к результату единицу и получим число в дополнительном коде:

101100012 + 1 = 101100102

6) в записи этого числа 4 единицы

 

Ответ: 2

 

8. Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Чему равно основание этой системы счисления N?

Решение 1: Начнем с двоичной системы. Для хранения числа 67 необходимо 7 цифр, т.к. 64<67<128. 128=27. Рассмотрим троичную систему. Для хранения числа 67 нужно 4 цифры, т.к. 27<67<81. 81=34. Следовательно, троичная система удовлетворяет условию: "число содержит 4 цифры". Теперь необходимо проверить, удовлетворяет данная система условию: "число оканчивается на 1". Для этого нужно перевести 6710 в троичную систему. Но полный перевод делать не надо, т.к. нас интересует только первый остаток, на него и будет оканчиваться 67 в троичной системе.

67| 3
6 22
7
6
1

Остаток равен 1. Следовательно, и второе условие выполнено, поэтому троичная система подходит. Основание троичной системы равно 3.

 

Ответ: 3

Решение 2: Так как запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1. Таким образом можно записать, что при некотором целом :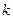

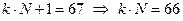
Из последнего выражения видно, что N (основание системы счисления) является делителем числа 66. Делителями числа 66 являются следующие натуральные числа: 2, 3,6, 11, 22, 33, 66.

Но нам известно, что запись числа содержит 4 цифры, то есть

Выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:

Видно, что из этого списка только для числа N = 3 выполняется условие 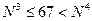. Таким образом, ответ – 3. Проверим это, переведя число 67 в троичную систему: 6710 = 21113

Ответ: 3

 

9. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:

1.ААААА
2.ААААО
3.ААААУ
4.АААОА
……

Запишите слово, которое стоит на 240-м месте от начала списка.

Решение:Из списка видно, что используются только символы: "А", "О", "У". Пусть "А"=0, "О"=1, "У"=2.

Список после замены станет таким:

1. 00000

2. 00001

3. 00002

4. 00010

 

Видно, что это числа, идущие по порядку от нуля в троичной системе. В десятичной системе счисления список бы был таким: 0, 1 , 2, 3.

Нам нужно найти, какое число будет стоять на 240 месте. Т.к. список чисел начинается с нуля, следовательно, нам нужно перевести число 239 в троичную систему счисления. Получим число: 222123. Переведем обратно в символы: УУУОУ.
Ответ: УУУОУ

 

10. В таблице ниже представлена часть кодовой таблицы ASCII:

Символ A B Q a b
Десятичный код
Шестнадцатеричный код

Каков шестнадцатеричный код символа “q” ?

Решение: Q-A=81-65=16 => q-a=16 => q-97=16 => q=97+16=113 => 11310 =7116

113| 16
112 7
1

 

Ответ: 71

 

11. Решите уравнение .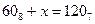
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.

Решение: Надо перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему:

1)

2) из уравнения 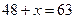получаем

3) переводим 15 в шестеричную систему счисления:

Ответ: 23

 

12. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?

 

Решение: если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело, поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 3 и на 5, то есть это число15.

Ответ: 15

 

13. Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.

Решение (вариант 1):