От светопроемов произвольной формы
Метод расчета основан на законе проекции телесного угла, в соответствии с которым:
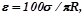% (70)
где s – проекция на освещаемую плоскость телесного угла W, под которым виден светопроем S из расчетной точки Т; R – радиус полусферы, в пределах которой измеряется телесный угол (рисунок 57).
Рисунок 57 –Схема к построению проекции телесного угла
Рассчитаем радиус круга из условия, что его площадь равна 40000 мм2. В результате получим R » 113 мм. В соответствию зависимостью (70) значение e = 0,01 % создает светопроем S, проекция телесного угла, под которым он виден на освещаемую плоскость, составляет 4 мм2. Исходя из этого, для расчета освещенности достаточно определить величину площади проекции телесного угла в полусфере радиусом R=113 мм и, зная, что ее площадь 4 мм2 составляет 0,01 %, рассчитать освещенность.
Величина радиуса полусферы подобрана с учетом удобства измерения площади проекции телесного угла, для чего можно использовать миллиметровую бумагу с величиной ячейки 2´2 мм. В этом случае площадь проекции телесного угла s = 1 см2 соответствует освещенности e » 0,25 %.
Для определения площади проекции телесного угла можно воспользоваться следующим способом. Допустим, есть разработанные в любом масштабе план, разрез, фасад и другие части проекта.
1. На условной рабочей поверхности (горизонтальная поверхность, размещенная на высоте 0,8 м от уровня чистого пола) или полу разместим расчетную точку Т и обозначим ее проекцию на плане через Т¢.
2. Из точки Т¢ как из центра проведем окружность радиусом 113 мм.
3. Выберем произвольную точку (А) на контуре светопроема и соединим ее прямой линией с точкой Т.
4. К проекции Т¢А¢ линии ТА на плане помещения из точки А¢. Проведем перпендикуляр и отложим на нем превышение точки А над освещаемой плоскостью.
5. Через полученную точку А¢¢ и точку Т¢ проведем прямую линию до встречи с окружностью и из точки встречи опустим перпендикуляр до линии Т¢А¢.
В результате получим проекцию a точки встречи линии ТА с поверхностью полусферы, то есть первую точку проекции телесного угла на освещаемую плоскость.
Аналогично следует определить достаточное количество проекций точек встреч с поверхностью полусферы линий, проведенных через контур светопроема и расчетную точку. Соединив полученные проекции точек плавной кривой, получим фигуру проекции на освещаемую плоскость телесного угла, под которым виден светопроем из расчетной точки.
Скопируем полученную фигурку на кальку и, наложив ее на миллиметровую бумагу (ячейки 2 мм), определим площадь, а затем – освещенность (можно строить фигуру проекции телесного угла на кальке, наложив ее на план).
Контрольные вопросы:
1. Природа света.
2. Световой поток.
3. Сила света.
4. Яркость.
5. Освещенность.
6. Прохождение света через атмосферу.
7. Коэффициент ослабления.
8. Оптическая толщина атмосферы.
9. Оптическая масса.
10. Взаимодействие света с веществом.
11. Коэффициент светопропускания.
12. Коэффициент отражения.
13. Коэффициент поглощения.
14. Виды естественного освещения.
15. Нормирование бокового естественного освещения.
16. Нормирование верхнего естественного освещения.
17. Последовательность расчета бокового освещения.
18. Последовательность расчета верхнего освещения.
19. Последовательность расчета комбинированного освещения.
20. Расчет геометрического коэффициента естественной освещенности по методу Данилюка.
ЛЕКЦИЯ 8 (3 часа)