Код вопроса 2811707

Однопролетная балка длиной l нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения на изгиб 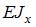 по длине постоянна. Угол поворота сечения А равен … (Влиянием поперечной силы при определении угла поворота пренебречь).
по длине постоянна. Угол поворота сечения А равен … (Влиянием поперечной силы при определении угла поворота пренебречь).

| |||

| |||

| |||

|
Решение:
При решении задачи воспользуемся интегралом Мора. Используя уравнения статики, определим реакции опор (рис. 1а).

Рассекаем балку произвольным сечением на две части и отбросим, например, правую часть. Действие отброшенной части заменяем внутренними силовыми факторами: поперечной силой  и изгибающим моментом
и изгибающим моментом  .
.
Составим выражение для определения изгибающего момента в произвольном сечении от внешней нагрузки 
Выражение для поперечной силы не составляем по условию задачи.
К сечению А, где необходимо определить угол поворота, прикладываем момент, равный единице, а внешнюю нагрузку отбрасываем (рисунок 2а).

Из уравнений статики найдем реакции опор от единичной нагрузки (рис. 2б). Произвольным сечением рассекаем балку на две части и отбрасываем также правую часть. Составим выражение для определения изгибающего момента в произвольном сечении от единичной нагрузки 
Выражения изгибающих моментов  и
и  подставим в интеграл Мора.
подставим в интеграл Мора.

После вычисления интеграла получим 
Знак «плюс» показывает, что сечение А поворачивается по направлению единичного момента.