Застосування теорії операційного числення до розв’язання диференціальних рівнянь.

Оригинал и изображение

Преобразованием Лапласа, называется соотношение

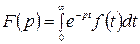
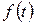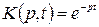которое ставит в соответствие дейст. переменного функцию комплексного переменного . Функция – ядро преобразования Лапласа, 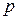– параметр преобразования.

Оригиналом называется комплексная функция 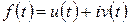действительного переменного , которая удовлетворяет условиям:

1. 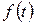– однозначно непрерывна или кусочно-непрерывная ф-ция вместе со своими производными 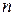-го порядка в интервале ;

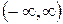2. 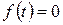, когда <0;

3. существуют такие постоянные 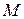>0 и , что для всех >0 < .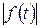

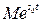Простейшим примером функции-оригинала есть единичная функция Хевисайда: .

Изображением функции-оригинала 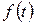называется функция комплексного переменного 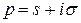, которая определяется інтегралом Лапласа:

 

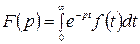
Свойства преобразования Лапласа:

1. Свойство линейности. Если и 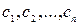– любые комплексные постоянные, то .

2. Теорема подобия. Если 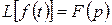и число >0, то .

3. Теорема запаздывания.Если 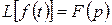и число >0, то .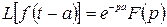

4. Теорема смещения.Есл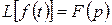и и 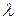– любое комплексное число, то .

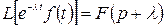5. Дифференцирование оригинала. Если 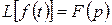и функции есть оригиналами, то

,

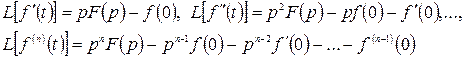где .

6. Дифференцирование изображения.Если 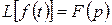, , 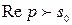то

7. Интегрирование оригинала.Если 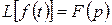, , 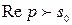то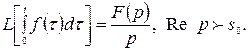

8. Интегрирование изображение. Если 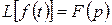, 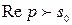и интеграл сходиться в полплощади , то , .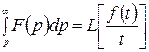

9. Изображение периодичного оригинала. Если 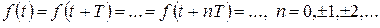, то 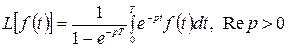.