Лінійні неоднорідні диференціальні рівняння 2го порядку зі сталими коефіцієнтами. Метод варіації довільних сталих.

 

Уравнение вида

,

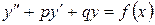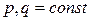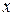где , - функция от и 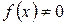, называется неоднородным диф-ным ур-нием 2го порядка с постоянными коэффициентами.

Метод вариации произвольных постоянных используется для нахождения частного решения лин. неоднороднного диф. ур. 2-го порядка с постоянными коэффициентами, при любом виде правой части . Суть решения:

1. Отыскивается общее решение соответствующего однородного уравнения ( т.е. ):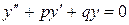

.

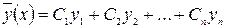2. Частное решение неоднородного диф. ур. ищется в виде:

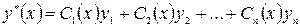
(т.е. 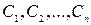заменяются на функции времени ).

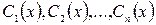3. Функции ( ) определяются из системы:

.

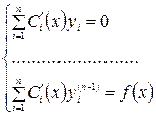4. Общее решение неоднородного ур. Определяется в виде суммы: общего решения однородного ур. 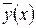и частного решения неоднородного ур. :

.

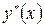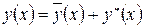Пример: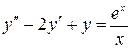

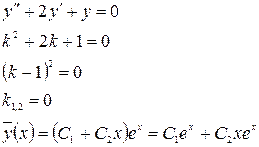
Пусть

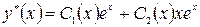
Определим неизвестные ф-ци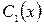и и 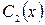из системы:

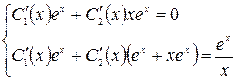
Решаем систему по методу Крамера:

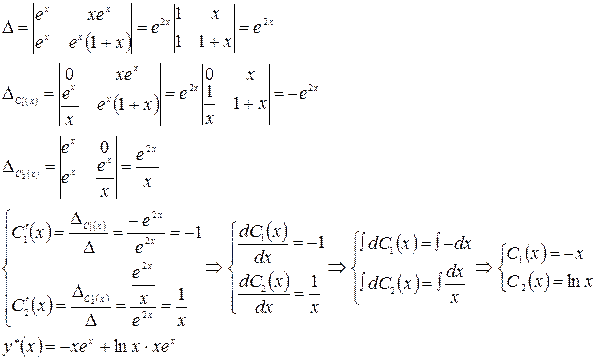
Общее решение

.

 

 

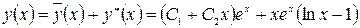70. Лінійні однорідні диференціальні рівняння 2го порядку зі сталими коефіцієнтами. Узагальнення на випадок рівняння 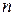-го порядку.

Уравнение вида

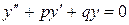(1)

где 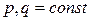(действительные), называется лин. однородным ур. 2го порядка с постоянными коэффициентами.

Для нахождения решения ур. (1) составляется характеристическое ур. вида:

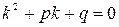(2)

и определяются корни данного квадратного уравнения, которые называются характеристическими числами. Структура общего решения ур (1) зависти от вида корней ур. (2).

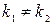1-ый вид: Корни действительные и различные , тогда общее решение ур. (1) имеет вид:

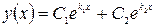
2-ой вид: Корни комплексно сопряженные 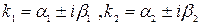, тогда общее решение ур. (1) имеет вид:

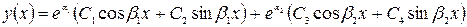
3-ий вид: Корни действительные и кратные(равные) 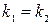, тогда общее решение ур. (1) имеет вид:

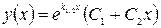
4-ый вид: Корни комплексно сопряженные кратные(равные) 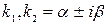, тогда ур. (1) имеет вид:

.

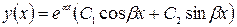Узагальнення на випадок рівняння 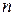-го порядку.

Уравнение вида

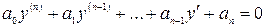(3)

где 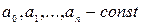(действительные), называется лин. однородным ур. 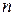-го порядка.

Для нахождения решения ур. (3) составляется характеристическое ур. вида:

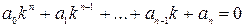(4)

и определяются корни его корни, , которые называются характеристическими числами. Структура общего решения ур. (3) зависит от вида корней ур. (4).

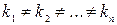1-ый вид: Корни действительные и различные , тогда общее решение ур. (3) имеет вид:

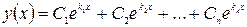
2-ой вид: Корни комплексно сопряженные 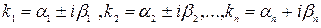, тогда общее решение ур. (3) имеет вид:

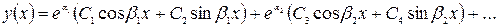
3-ий вид: Корни действительные и кратные(равные) 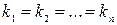, тогда общее решение ур. (3) имеет вид:

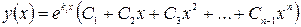
4-ый вид: Корни комплексно сопряженные кратные(равные) , тогда ур. (3) имеет вид:

.
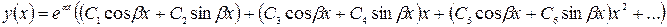