Нахождение точек перегиба.

Точками перегиба могут служить только критические точки, принадлежащие области определения функции y=f(x), в которых вторая производная f ^''(x) обращается в нуль или терпит разрыв. Если при переходе через критическую точку х=х₀ вторая производная f ^''(x) меняет знак, то график функции имеет точку перегиба (х₀; f(x₀)).

Пример 5. Найти точку перегиба кривой f(x)=6x²-x³.

Решение:

f ^'(x)=12x-3x²

f ^''(x)=12-6x

f ^''(x)=0 12-6x=0

-6x=-12

x=2

f(2)=6∙2²-2³=24-8=16

(2;16) – точка перегиба.

Схема исследования функции.

1. Найти область определения функции y=f(x);

2. Исследовать функцию на четность и нечетность;

3. Исследовать функцию на периодичность;

4. Исследовать функцию на непрерывность, найти точки разрыва;

5. Найти критические точки первого рода;

6. Найти интервалы монотонности и экстремумы функции;

7. Найти критические точки второго рода;

8. Найти интервалы выпуклости и точки перегиба;

9. Найти асимптоты графика функции;

10. Найти точки пересечения графика функции с осями координат;

11. Построить график.

Задания

Вариант 1 Вариант 2

1. Найти промежутки возрастания и убывания функции:

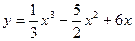
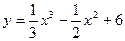
2. Исследовать на экстремум и точки перегиба кривую:

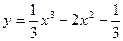
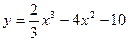
Построить схематический график этой функции.

 

3. Исследовать на выпуклость кривую:

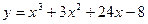
Контрольные вопросы:

1. Дайте определения точке перегиба.

2. Как определить промежутки выпуклости графика функции?

3. Сформулируйте признаки монотонности функции.