Геометрический смысл производной

Литература

1. Богомолов Н.В. Сборник дидактических заданий по математике. – М.: Дрофа,2009

2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов.- М.: Наука, 2009

3. П.М. Апанасов, М.И.Орлов Сборник задач по математике

Методические указания

Физический смысл

При прямолинейном движении точки скорость V в данный момент t = 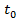есть производная 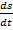от пути s по времени t, вычисленная при t = :

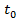V=S’(t)

Ускорение a в данный момент t = 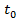есть производная 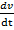от скорости V по времени t, вычисленная при t = .

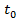Геометрический смысл производной

Пусть дана функция у = f(x) и касательная к графику в точке А(а;f(a)), тогда значение производной функции у = f(x) в точке х = а равно угловому коэффициенту k = (k = tgα), касательной к графику функции у = f(x) в точке х = х₀. В этом состоит геометрический смысл производной.

k = f’(x₀)

Уравнение касательной к кривой у = f(x) в точке М₀(х₀;у₀) имеет вид

у-у₀= f’(x₀)(х-х₀).

Уравнение нормали к кривой у = f(x) в точке М₀(х₀;у₀) имеет вид

у-у₀= 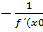(х-х₀).

Пример 1. Найти угол, который образуют с осью х касательная к графику функции y = 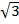sin , проведенная в точке х=0.

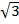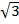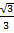Решение: f(x)= sin , f’(x)= cos ∙ = cos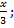

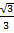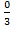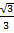при а=0 f’(x)= cos = cos0= .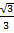

Значит, k = 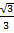, т.к. k=tgα, tgα= 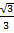, откуда α=30⁰.