Формулы Бейеса.

Практическое занятие № 6

Формула полной вероятности. Формула Байеса.

Формула полной вероятности. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий 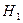, , 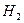…, , образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A.

Формулы Бейеса.

Пусть событие A может наступить при наступлении одного из несовместных событий 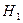, , 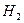…, , образующих полную группу событий. Поскольку заранее неизвестно, какое из событий наступит, их называют гипотезами. Допустим, что событие A наступило. Надо определить, как изменились вероятности гипотез:

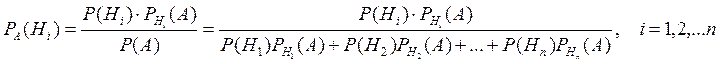
Пример 1. Компьютеры одной марки производят 2 предприятия. Первое предприятие выпускает 3/4 всех компьютеров, второе -1/4. На первом предприятии 1% брака, на втором – 2%. Найти вероятность того, что купленный вами компьютер не исправен.

Решение.Пусть событие А–купленный компьютер не исправен. Полнаягруппа событий, необходимая для применения формулы полной вероятности, состоит из двух событий: 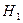– «компьютер куплен на первом заводе» и 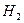– «компьютер куплен на втором заводе».

По условию задачи

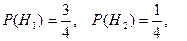
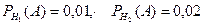- вероятности брака соответственно на 1-ом и 2-ом предприятии.

Тогда, согласно формуле полной вероятности,вероятность купить бракованный компьютер, равна

Пример 2.В первойкоробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке –10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.

Решение.Обозначим через А событие – из первой коробки извлечена стандартная лампа.

Из второй коробки могла быть извлечена либо стандартная лампа (событие 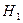), либо нестандартная (событие ).

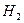Вероятность того, что из второй коробки извлечена стандартная лампа,

Вероятность того, что из второй коробки извлечена нестандартная лампа,

Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа равна

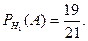
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа равна

Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна

Пример 3. На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй – 46% и третьей – 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, для третьей – 1%. Найти вероятность того, что наудачу взятое нестандартное изделие произведено на первой фабрике.

Решение. Обозначим через А событие, состоящее в том, что взято нестандартное изделие, через 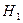, , 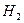– гипотезы, состоящие в том, что взято изделие, изготовленное соответственно на первой, на второй, на третьей фабрике.

Из условия задачи следует, что

Поскольку в данном случае

то в соответствии с формулой Байеса находим искомую вероятность

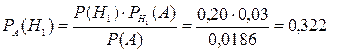
Замечание. Аналогично находятся вероятности:

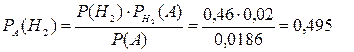
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

На фабрике, изготавливающей болты, первая машина производит 30%, вторая –25%, третья –45% всех изделий. Брак в их продукции составляет соответственно 2%, 1%, 3%. Найдите вероятность того, что случайно выбранный болт оказался стандартным. Ответ: 0,6.
На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,2% брака, второй –0,3% и третий –0,4%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 500, со второго –1000 и с третьего –1500 деталей. Ответ: 0,003.
Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,01, для второго – 0,02, для третьего –0,03. Обработанные детали складываются в один ящик. Производительность первого станка в два раза больше, чем второго, а третьего в три раза меньше, чем второго. Какова вероятность того, что взятая наугад деталь будет бракованной? Ответ: 0,015.
На складе находятся детали, изготовленные на двух заводах. Известно, что объем продукции первого завода в 4 раза превышает объем продукции второго завода. Вероятность брака на первом заводе равна 0,05, на втором заводе –0,01. Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена на первом заводе? Ответ: 0,953.
В первой урне 2 голубых и 6 красных шаров, во второй – 4 голубых и 2 красных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар. 1) Какова вероятность того, что этот шар голубой? 2) Предположим, что шар, взятый из второй урны, оказался голубым. Какова вероятность того, что из первой урны во вторую были переложены 2 голубых шара? Ответ:
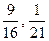
Имеется три урны. В первой урне 6 белых и 4 черных шара, во второй – 5 белых и 5 черных шара, в третьей – 7 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. 1) Найти вероятность того, что шар – белый. 2) Найти вероятность того, что он вынут из третьей урны.
Два автомата производят детали, которые поступают на общий конвейер. Первый автомат производит 40% всех деталей, второй - 60% деталей. Вероятность изготовления стандартной детали первым автоматом равна 0,95, вторым – 0,8. Найти вероятность того, взятая наугад деталь – стандартная.
Студент в поисках книги посещает три библиотеки. Вероятности того, что книга есть в библиотеках, соответственно равны: 0,5, 0,3, 0,2. Какова вероятность того, нужная книга найдена.
Имеется две урны. В первой 3 белых и 4 черных шара, во второй – 4 белых и 2 черных шара. Из случайно выбранной урны извлекается шар. Найти вероятность того, что он оказался черным.
Имеется две урны. В первой 4 белых и 3 черных шара, во второй – 5 белых и 2 черных шара. Из случайно выбранной урны извлекается шар, который оказался черным. Найти вероятность того, что он вынут из первой урны.
Имеются три одинаковые на вид урны; в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.
Два стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.

Ответить на следующие вопросы:

1. Что называют событием? Какое событие называют достоверным, невозможным, случайным в данном опыте?

2. Какие события называют совместными (несовместными) в данном опыте?

3. Какие события называют противоположными?

4. Какие события называют равновозможными?

5. Что называют полной группой событий?

6. Какие элементарные исходы называют благоприятствующими данному событию?

7. Что называют вероятностью события?

8. Чему равна вероятность достоверного, невозможного события?

9. В каких пределах заключена вероятность случайного события?

10. Что называют перестановками?

11. По какой формуле вычисляют число перестановок из n различных элементов?

12. Что называют размещениями?

13. По какой формуле вычисляют число размещений из n различных элементов по m элементов?

14. Что называют сочетаниями?

15. По какой формуле вычисляют число сочетаний из n различных элементов по m элементов?

16. Что такое частота события?

17. Какое определение вероятности называют статистическим?

18. Что называют суммой двух событий?

19. Что называют суммой нескольких событий?

20. Что называют произведением двух событий?

21. Что называют произведением нескольких событий?

22. Чему равна вероятность суммы двух несовместных событий?

23. Чему равна вероятность суммы двух совместных событий?

24. Чему равна сумма вероятностей событий, образующих полную группу?

25. Чему равна сумма вероятностей противоположных событий?

26. Как определяется независимость двух событий?

27. Чему равна вероятность произведения двух независимых событий?

28. Сформулируйте теорему о вероятности произведения зависимых событий.

29. Сформулируйтетеорему о вероятности появления хотя бы одного из n событийнезависимых в совокупности.

Вариант № 1.

1. Что называют событием? Какое событие называют достоверным, невозможным, случайным в данном опыте?

2. Что называют вероятностью события?

3. Что называют перестановками?

4. Чему равна вероятность суммы двух несовместных событий?

5. Чему равна сумма вероятностей событий, образующих полную группу?

Вариант № 2.

1. Какие события называют совместными (несовместными) в данном опыте?

2. Чему равна вероятность достоверного, невозможного события?

3. По какой формуле вычисляют число перестановок из n различных элементов?

4. Как определяется независимость двух событий?

5. Сформулируйтетеорему о вероятности появления хотя бы одного из n событийнезависимых в совокупности.

Вариант № 3.

1. Какие события называют противоположными?

2. В каких пределах заключена вероятность случайного события?

3. Что называют размещениями?

4. Что называют суммой двух событий?

5. Сформулируйте теорему о вероятности произведения зависимых событий.

Вариант № 4.

1. Какие события называют равновозможными?

2. Что такое частота события?

3. По какой формуле вычисляют число размещений из n различных элементов по m элементов?

4. Что называют суммой нескольких событий?

5. Чему равна вероятность произведения двух независимых событий?

Вариант № 5.

1. Какие элементарные исходы называют благоприятствующими данному событию?

2. Какое определение вероятности называют статистическим?

3. Что называют сочетаниями?

4. Что называют произведением двух событий?

5. Чему равна сумма вероятностей противоположных событий?

Вариант № 6.

1. Что называют полной группой событий?

2. Что называют вероятностью события?

3. По какой формуле вычисляют число сочетаний из n различных элементов по m элементов?

4. Что называют произведением нескольких событий?

5. Чему равна вероятность суммы двух несовместных событий?

1. Определение случайного события. Невозможное и достоверное события.

2. Взаимно противоположные события. Полная группа событий.

3. Совместные и несовместные события.

4. Зависимые и независимые события.

5. Классическое определение вероятности равновозможных событий.

6. Основные свойства классической вероятности.

7. Относительная частота случайного события.

8. Статистическая вероятность.

9. Определение суммы двух и более случайных событий.

10. Определение произведения случайных событий.

11. Формула для вероятности суммы двух несовместных случайных событий

12. Формула для вероятности суммы двух совместных случайных событий.

13. Вероятность полной группы событий. Вероятность противоположных событий.

14. Условная вероятность. Независимые случайные события.

15. Формула для вероятности произведения случайных событий.

16. Формула для вероятности наступления хотя бы одного из событий независимых в совокупности.

17. Перестановки. Формула перестановок.

18. Сочетания. Формула сочетаний.

19. Размещения. Формула размещений.