Лекция.
Математикалық ұғымдарды меңгеру
1.Математикалық ұғымдарды қалыптастыру.
2.Математикалық ұғымдарды ендіру жолдары
1. Математикалық ұғымдарды қалыптастыру.
Математиканы оқып-үйрену ұғымды қалыптастыру мен оны терең танымдық дәрежеге жеткізуден, математикалық тұжырымдарды, теоремаларды дәлелдей білуге үйретуден және оны нақтылы іс-әрекетте, есеп шығаруға қолдана білуден тұрады. Мұның алғашқысы да, маңыздысы да математикалық ұғымдарды қалыптастыру болғандықтан, оның алатын орны да ерекше. Оқушының бар білім-танымының бастауы, оның қолданылар аясының кеңдігі мен ауқымдылығы алғашқы мәліметтердің қалай түсіндіріліп, жеткізілгеніне байланысты.
Мектеп оқушыларының бойында ғылыми ұғымдар жүйесін қалыптастыру – оларды жалпы ғылыми білімдер жүйесімен қаруландырудың маңызды элементтерінің бірі. Әрбір оқу пәні бір-бірімен өзара байланыстағы ұғымдар жүйесін қамтиды. Оқушылардың жалпы пән бойынша білімдерінің сапасы олардың ұғымдар жүйесін меңгеруіне байланысты. Заттардың қасиеттері мен сипаттарын, материя қозғалысының формалары мен олардың алуан түрлі көріністерін оқып-үйрену, математика және жаратылыстану пәндері мектептік курсының мазмұны болып табылады.
Ұғымдарды меңгермейінше заңдар мен теорияларды саналы түрде білу мүмкін емес. Ғылыми зерттеулер мен адамның практикалық қызметінде кеңінен қолданылып жүрген, ғылымның “қаруы” ретінде қабылданған ұғымдардың мазмұны оқу үдерісінде біртіндеп ашылады. Математикалық ұғымдар жалпылау мен абстракциялаудың жоғары деңгейі болғандықтан мектеп курсында оған ерекше орын береді. Математикалық ұғымдарды қалыптастыру оқушылардың белсенді іс-әрекетінсіз мүмкін емес. Математикалық ұғымдарды игеру таным үрдісінің жалпы және нақтылы іс-әрекеттері арқылы жүзеге асырылады. Оларға жалпылау, нақтылау, анализ, синтез, салыстыру, аналогия, жіктеу және бір жүйеге келтіру іс-әрекеттері жатады.
Математикалық ұғымдардың қалыптасуы күрделі психологиялық үдеріс. Ұғымдардың қалыптасуы мынадай сүлбе бойынша жүреді:
сезіну (түйсіну) → қабылдау → түсінік (елестету) → ұғым.
Сезіну, қабылдау және түсінік – танудың алғашқы сатысы, ол сезімдік тану деп аталады. Сезіну – сыртқы дүние заттары мен құбылыстарының жеке белгілерінің мидағы бейнеленуі. Сол себепті сезіну шындықты танып білудің алғашқы сатысы болып табылады. Сезінумен тікелей байланыста қабылдау жүзеге асырылады. Қабылдау – заттар мен құбылыстардың мидағы тұтастай бейнеленуі. Қабылдау кезінде ми қабығының аналитикалық-синтетикалық қабілеті айқын көріне бастайды.
Ұғымның санада пайда болуының жоғарырақ сатысы – түсінік. Түсінік еске сақтаумен тікелей байланысты. Түсінік заттың бұрын қабылданған бейнесін қайталау. Ми қыртыстарында қозу нәтижесінде бұрынырақ сақталып қалған іздер – түсініктің физиологиялық негізі болып табылады.
Түсініктің пайда болуында ойлаудың аналитикалық-синтетикалық қызметі айқындала түседі: қабылдаудағы жалпы элементтер бөліктерге бөлінеді де, онымен бір мезгілде ол элементтер бір бүтінге, яғни қандайда бір бейнеге біріктіріледі. Түсінік сезіну мен қабылдаудан тыс бола алмайды.
Ұғымның құралуы түсінікке негізделеді.
Ойлаудың негізгі элементі – ұғым. Ұғым – объективті шындықтың көңіл аударарлықтай және жалпыланған маңызды қасиеттерін бейнелейтін ойлау формасы. Әрбір ұғымға біздің қабылдауымызда және түсініктерімізде бейнеленетін материалдық дүние объектілерінің біршама класы сәйкес келеді.
Ұғым қалыптасуының осы сатыларын “квадрат” ұғымы арқылы көрсетелік.
7-8 жасар балаларға алдымен әр түрлі бояулармен боялған, әр түрлі пішіндегі, әр түрлі өлшемдегі квадрат, квадрат емес фигуралар көрсетіледі. Олардың ішінен бір квадратты жеке алып, мынау – квадрат дейміз. Сонан соң қалған фигуралардан квадратты тап десе, балалар пішініне, түсіне, мөлшеріне көңіл аудармай, квадраттарды қиналмай-ақ табады. Әрі қарай фигураларды жинап алып, “квадрат сыз” десек, балалар квадрат болатындай фигура сызуға әрекеттенеді. Бұл квадрат туралы түсініктің пайда болуы. Содан соң “квадратты басқа фигуралардан” қалай айыруға болады деген сұраққа “оның 4 қабырғасы”, “4 бұрышы болады, қабырғалары өзара тең, бұрыштары тік болады” деп жауап береді. Яғни ойлау үдерісі нәтижесінде оның өзіне тән қасиеті ерекшеленіп, түсініктен квадрат ұғымы пайда болады. Ұғымның даму диалектикасы да осында.
Ұғымның көрнекілік дәрежесі қабылдау мен түсініктегідей бола алмайды. Оның себебі, ұғымда объектінің барлық қасиеттері емес, оның тек айрықша, ең жалпы қасиеттері ғана бейнеленеді. Объектіні басқа объектілерден өзгешелеп (ерекшелеп) тұратын ең жалпы белгілері ұғымның елеулі(мәнді)белгілері деп аталынады. Мысалы, параллелограмның елеулі белгілері – оның қарама-қарсы қабырғаларының параллельдігі, қарама-қарсы қабырғаларының теңдігі, қарама-қарсы бұрыштарының теңдігі т.б. бола алады.
Ұғымның елеулі белгілерін оның қасиеттерінен ажырата алу керек. Ұғымның белгілері сол ұғымды қамтып тұрған объектілер класын бөліп алуға мүмкіндік берсе, оның қасиеттері сол ұғымның өзіне ғана тән болады. Ұғымның қасиеттері әр уақытта оның белгілері бола бермейді. Мысалы, вертикаль бұрыштардың өзара тең болатын қасиеті, вертикаль бұрыштарды анықтай бермейді, себебі бұрыштар тең болғанымен, олар вертикаль бұрыштар болмауы да мүмкін. Ұғымның белгілері оның қасиеттерімен дәл келсе, ұғымның қажетті және жеткілікті шартын құрайды.
Ұғымды басқа ұғымдардан ажыратып тұратын белгілері біреу ғана болмауы мүмкін. Жоғарыда келтірілген параллелограмм белгілерінің кез келгенін параллелограмм анықтамасының негізі ретінде алуға болады. Анықтаманы тұжырымдау үшін белгілерінің, сол ұғымды анықтауға жеткілікті біреуі ғана немесе бірнешеуі алынады да, қалғандары сол анықтамадан шығатын логикалық салдар ретінде қатаң түрде дәлелденеді.
Тілдің ұғымдарды қалыптастыру мен дамытудағы маңызы да ерекше. Әрбір ұғым сол ұғымға сәйкес келетін терминмен байланысты. Терминдерге мағына беру анықтама немесе түсініктеме арқылы жүзеге асырылады. Сонымен бірге математикалық ұғымдар символдық (белгілермен) белгілеулермен де таңбаланады. Ұғымдарды белгілейтін символдық мағынасы сол ұғымның өзі. Мысалы, “Бір жазықтықта жататын және қиылыспайтын екі түзу” – “паралелль” терминімен және “| |” символымен белгіленеді, ал “жазықтықтағы үш нүкте және оларды қосатын үш кесіндіден тұратын фигура “үшбұрыш” термині және “Δ” символы арқылы белгіленеді.
Оқыту үдерісінде жаңадан енгізілген әрбір термин және символ оқушыларға үйреншікті болып қалатындай және оларды қажетті жерлеріне еркін, ешқандай қиындықсыз қолдана беретіндей дәрежеде игерілуі қамтамасыз етілуі қажет. Терминдер мен оларға сәйкес келетін символдарды саналы қолдана білу оқушылардың мектеп математика курсын тиянақты меңгеруінің негізін қалайды.
Математикалық терминдер екі түрлі болады:
1) халықаралық (интернационалдық) терминдер;
2) ана тілі негізінде қалыптасқан терминдер.
Математикалық ұғымдарға оқыту барысында терминдердің мағынасын және олардың ұғыммен байланысын айқындап түсіндіріп отырудың маңызы ерекше.
Ұғымның анықтамасын тұжырымдаумен оқушылардың санасында ұғымның қалыптасуы аяқталмайды. Ұғымның қалыптасқандығы оның елеулі қасиеттерін оқушылардың анықтай алуымен, олардың арасындағы байланыстарды көрсете білуімен, ол ұғымды әр түрлі жағдайларда қолдану, түрлі сипаттағы жаттығуларды орындау және басқа пәндерде пайдалана білуімен т.б. сипатталады.
Ал ұғымды меңгеру дегеніміз – болмыстың, заттар мен құбылыстардың маңызды қасиеттерін, олардың арасындағы мәнді байланыстарды, арақатынастарды білу.
Ұғымды меңгеру оқушылардың белсенді ой қызметімен, анализ және синтез, салыстыру, абстракциялау және жалпылау сияқты ойлау амалдарын (операцияларын) орындаумен байланысты. Сондықтан ұғымдарды қалыптастыру оқушылардың ойлауын дамытумен тікелей байланысты.
Математикалық ұғымдарды игеру оқушының нерв жүйесінің аналитикалық-синтетикалық қызметінің нәтижесі ретінде түсіндіріледі. Талдау арқылы оқушы заттар мен құбылыстардың жекелеген қасиеттерін бөліп алады, ал синтез көмегімен жалпы белгілер бойынша оларды біріктіреді. Одан соң объектінің ерекше қасиеттері абстракцияланып, терминдермен бекітіледі. Бұл үдеріс бөлініп алынған ұғымды қолдана білумен аяқталады.
Ұғымды енгізу
Оқыту үрдісінде ғылыми ұғымдарды енгізу, анықтама беру екі жолмен жүзеге асырылады:
1) нақтылы-индуктивті,
2) абстрактілі-дедуктивті.
Бірінші жолда ұғымның анықтамасы бірден тұжырымдалмайды.
1. Жаңадан енгізілген ұғымның бейнесі болатындай жеткілікті мөлшердегі объектілерді қарастыру және оларға бақылау жасау, оқушылардың өмірлік тәжірибесі мен алған білімдерін пайдалану, нәтижеде қабылдау, алғашқы түсініктер пайда болады.
2. Ұғымға ата беріледі, терминмен таныстырылыды.
3. Ұғымның елеулі қасиеттерін ажыратып көрсету және анықтаманы оқушылардың өздері тұжырымдауды ұйымдастыру;
4. Қарастырылып отырған ұғымның дәл анықтамасын тұжырымдау.
5. Ұғымның символдық белгілеуі бар болса, символды енгізу.
6. Ұғымды оқытылып отырған курстың ұғымдар жүйесіне қосу (бұл кезең пәнішілік байланысты жүзеге асыру болып табылады).
7. Енгізілген ұғымды практикалық қолдану (бұл жерде оқытылып отырған ұғымның нақты жағдайлардағы, аттас пәндердегі қолданылуы туралы мәселе қойылып отыр, ол пәнаралық байланысты жүзеге асырады).
Екінші жол бойынша ұғымның анықтамасы алғашқы түсініктемелер жасалынбай, дайын түрде тұжырымдай отырып енгізіледі.
Бұл негізінен орта және жоғарғы сыныптарда пайдаланылады. Бірақ И.Ф.Тесленконың пікірінше, “Бұл екі жол да диалектикалық таным үрдісінің қажетті бөліктері болып табылады”, сондықтан жаңа ұғымдарды енгізуде бұл екі жолдың екеуіне де қатаң шек қоюға болмайды.
Сұрақтар:
1.Математикалық ұғымдарды қалыптастыру.
2.Математикалық ұғымдарды нақтылы-индукивті жолмен енгізу.
3.Математикалық ұғымдарды абстрактілі-дедуктивті жолмен енгізу.
Пайданылған әдебиеттер
1.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж
2. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж
3. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003
18- лекция.
Математикалық сөйлемдер.
1. Аксиома.
2. Постулат.
3.Теорема және оларды түрлері
Математикалық сөйлемдер
Мектеп математика курсында математикалық сөйлемнің мынадай түрлері кездеседі: аксиома; постулат; теорема; лемма; салдар.
Аксиома грекше axioma сөзінен алынған, оның сөздік мағынасы “ақиқатқа ие болған сөйлем”. Сондықтан да аксиомаға мектеп математика курсында мынадай анықтама берілген: “Дәлелдемесіз алынатын математикалық сөйлемдерді аксиома дейді”.
Аксиома негізінен ең қарапайым геометриялық фигура немесе қарапайым математикалық ережелердің негізгі қасиеттерін өрнектейтін сөйлем.
Мысал келтірейік: мектеп геометрия курсында қабылданған мынадай аксиомалар бар:
“Екі нүктені бастыра тек бір ғана түзу жүргізуге болады” және “Екі түзу тек бір ғана нүктеде қиылысады”. Бұл екі сөйлемнің екеуі де ақиқаттығы жағынан бірдей десек болады. Бірақ, бұл екеуін бірдей аксиомалар тізіміне енгізуге болмайды. Өйткені, егер бірінші сөйлемді аксиома етіп алсақ, онда оған сүйеніп екіншісін дәлелдеуге болады. Шынында да, егер екі түзу екі нүктеде қиылысады деп қарсы жорысақ, онда екі нүктені бастыра екі түзу жүргізуге болатын болып шығады. Ал бұл аксиома етіп алынған бірінші сөйлемге қайшы келеді. Сондықтан екі түзудің екі нүктеде қиылысуы мүмкін емес. Мұндай жағдайда екінші сөйлемді бірінші сөйлемнің салдары немесе екіншісі біріншісіне тәуелді дейміз. Мұнан аксиома етіп алынған сөйлемдер бір-біріне тәуелсіз болу керек деген қорытынды шығады.
Сонымен аксиомаларға қойылатын бірінші талаптың тұжырымдамасы – олар тәуелсіз болуы керек.
Аксиомаларға қойылатын екінші талап оларда қайшылық болмау керек.Мұны былай түсінеміз: Біріншіден, аксиомалар қатарына енгізілген сөйлемдердің ішінде бірінің ақиқаттаған пікірін жоққа шығаратын екінші аксиома болмау керек. Мысалы, “Берілген түзуден тыс жатқан нүктеден осы түзуге тек бір ғана параллель түзу жүргізуге болады” деген аксиомаға қосып, “берілген түзуден тыс жатқан нүкте арқылы осы түзуге параллель бірде-бір түзу жүргізуге болмайды” деген пікірді аксиома етіп алуға болмайды.
Аксиомаларға қойылатын үшінші талап – аксиомалар системасы толық болу керек.
Мұны былай түсінуге болады: егер аксиомалар системасы толық болмаса, онда оларға қосымша алғашқы аксиомаларға қайшы келмейтін және оларға тәуелсіз болатын аксиома қосуға болады, ал толық болса, онда жаңадан енгізілген аксиома не оларға тәуелді болады да, не оларға қайшы келеді.
Мектеп геометрия курсында төмендегі аксиомалар системасы бар:
1. Тиістілік аксиомасы:
а) Кез келген түзу сызық нүктелер жиынынан тұрады.
ә) Кез келген екі нүкте арқылы түзу жүргізуге болады және ол тек біреу ғана болады.
б) Қандай түзуді алсақ та, ол түзуге тиісті нүктелер де, оған тиісті емес нүктелер де бар болады.
2. Ара қашықтық аксиомасы:
а) Кез келген кесіндінің ұзындығы өзінің кез келген нүктесімен бөлінген бөліктері ұзындықтарының қосындысына тең болады.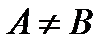 
болса, 
, 
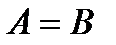болса, 
.
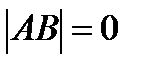б) А нүктеден В нүктеге дейінгі ара қашықтық В нүктеден А нүктеге дейінгі ара қашықтыққа тең: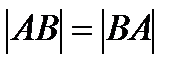 
.
в) Кез келген үш А, В, С нүкте үшін А-дан С-ға дейінгі ара қашықтық А-дан В-ға және С-ға дейінгі ара қашықтықтардың қосындысынан артық емес: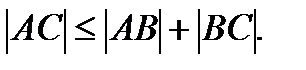 
3. Реттілік аксиомасы:
а) Түзудегі үш нүктенің біреуі және тек қана біреуі қалған екеуінің арасында жатады.
б) Түзу жазықтықты екі жарты жазықтыққа бөледі.
4. Қозғалыс аксиомасы.
а) Егер (АВ) ара қашықтық оң болып, ол (А1 В1) ара қашықтығына тең болса, онда А нүктесі А1 нүктесіне және В нүктесін В1 нүктесіне бейнелейтін тек бір ғана қозғалыс бар болады.