Линеаризация физических систем
Условие линейности- линейная связь возмущения x(t) и реакции y(t)
- x1(t) ↔ y1(t)
x2(t) ↔ y2(t) x1(t)+x2(t)↔y1(t)+y2(t)
принцип суперпозиции.
- ax (t)→ay(t) –принцип гомогенности
- Линейная система должна удовлетворть принципам суперпозиции и гомогенности.
y=x2 (не выполняется 1 принцип)
y=mx+b (не выполняется 2 принцип)
но в окрестности р.т. х0,у0 при ∆х, ∆у→0
х=х0+∆х, у=у0+∆у у0=mx0+b
у0+∆у= mx0+∆хm+b
∆у=m∆х
Мех. и электрические элементы линейны в достаточно широком диапазоне изменения переменных, но не гидравл. и тепл.
При условии ∆х, ∆у→0 систему можно линеаризировать.
Пусть y(t)=g{x(t)}Р.т. x0 Разложение Тейлора в окрестностях рабочей точки х 0
 тогда при ∆x=(x-x0)
тогда при ∆x=(x-x0) 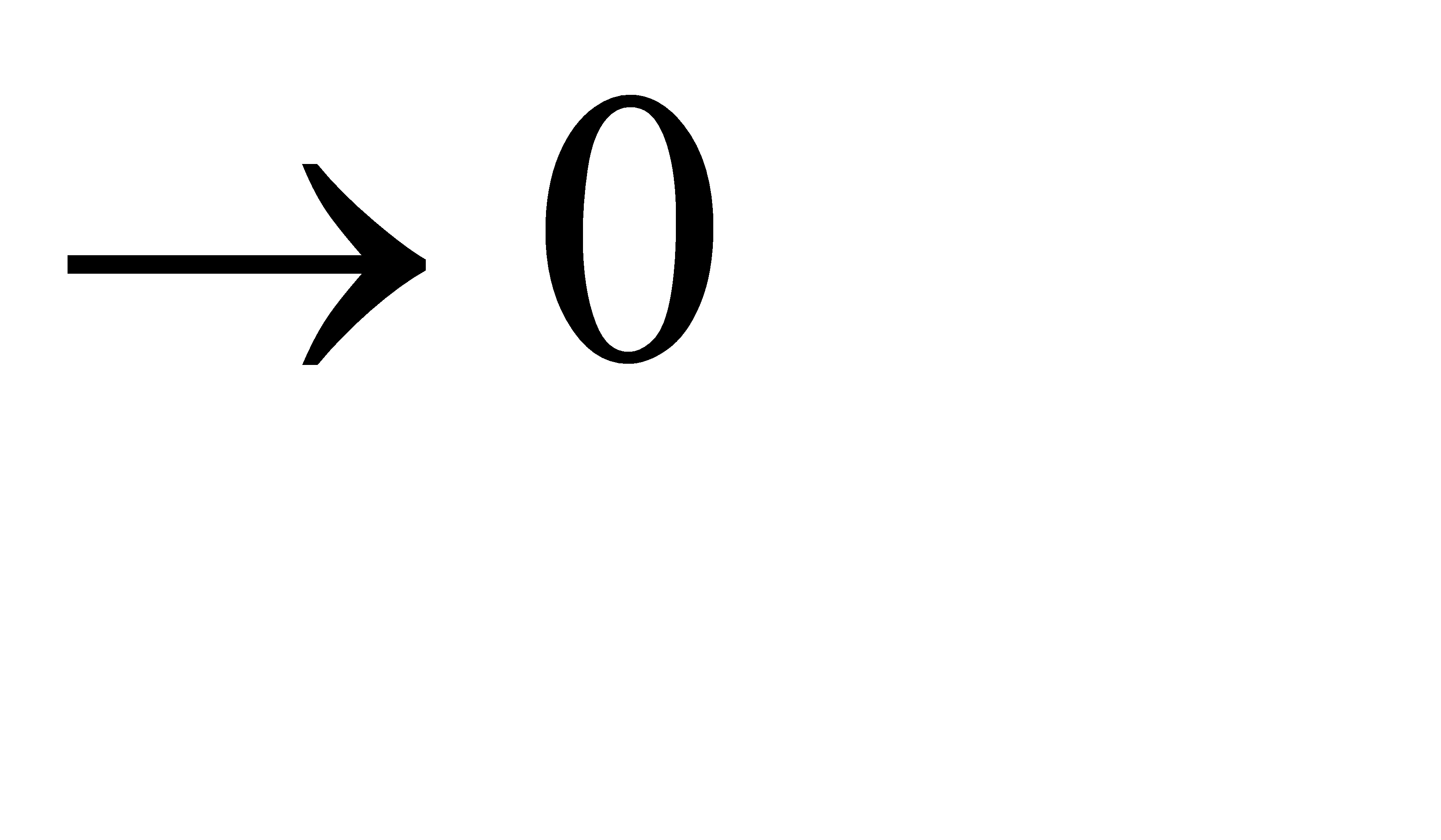


y-y0=m(x-x0) ∆y=m∆x

В Р.т (пол. равновесия) f0=Mg если для пел. пружины. f=y2, то
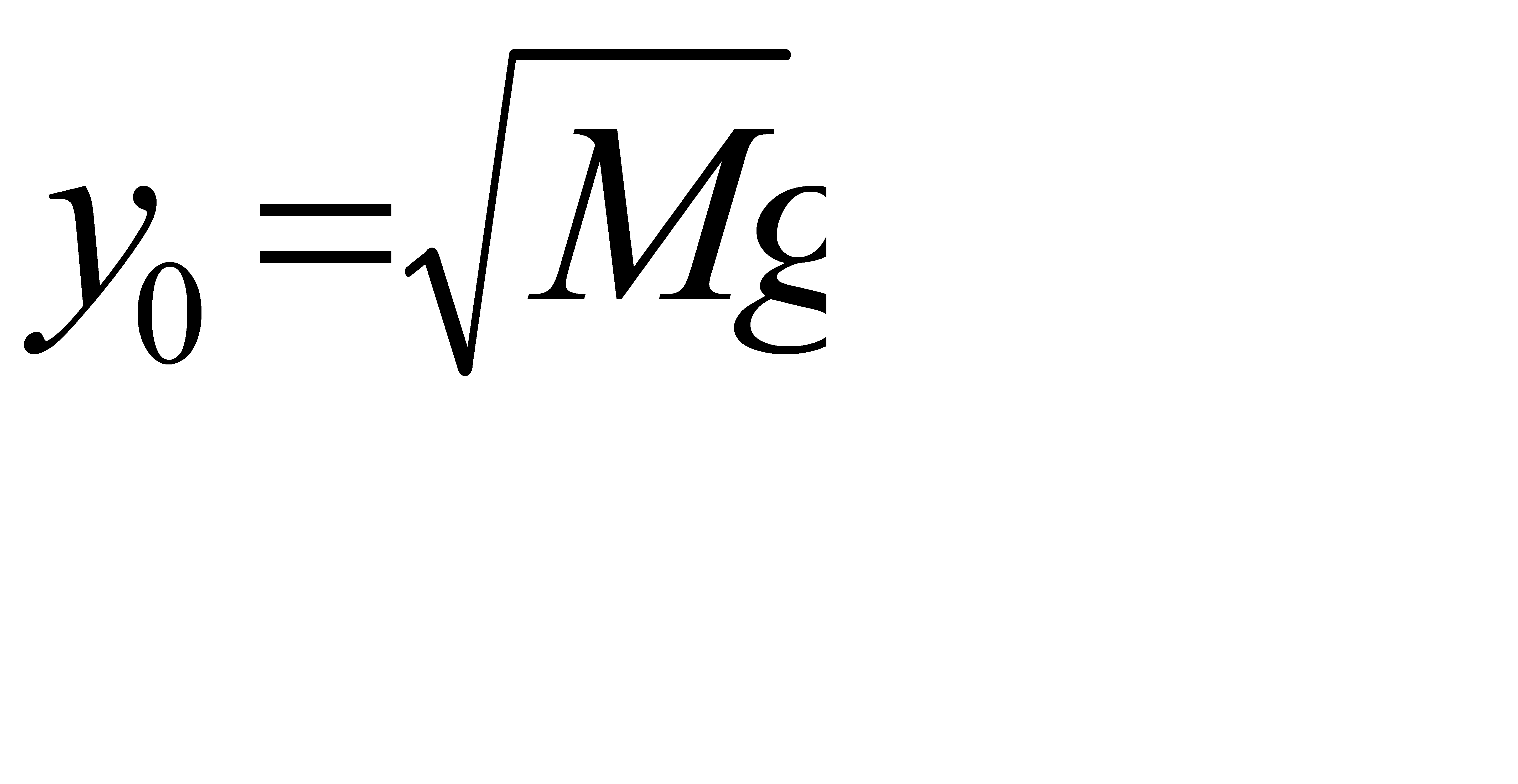
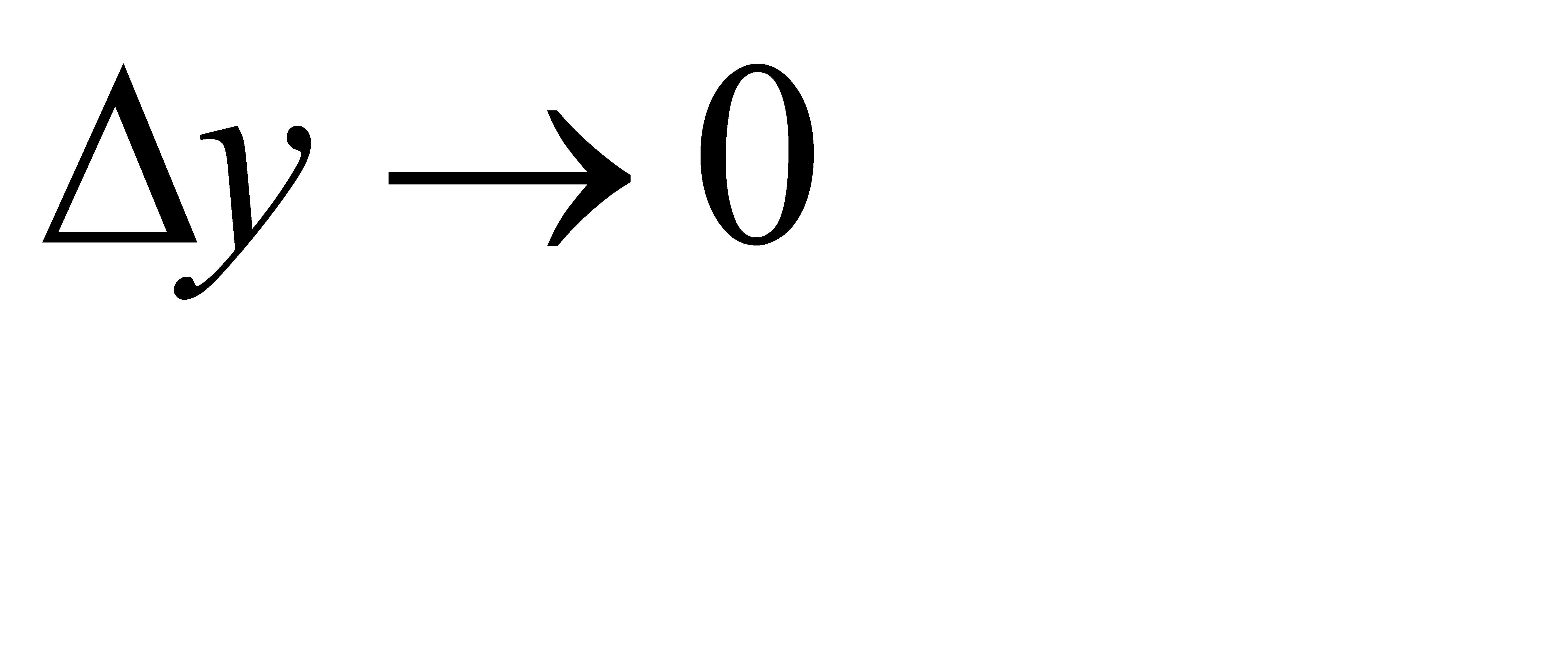
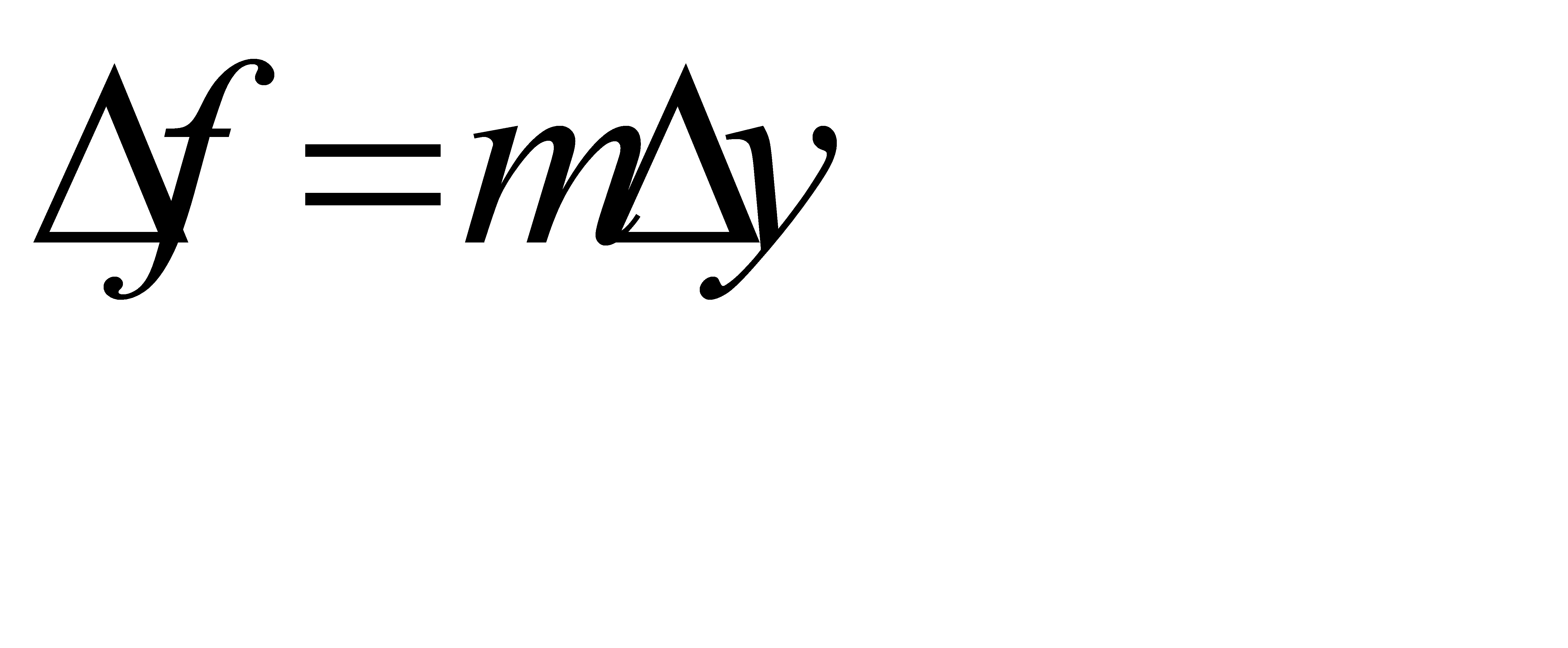
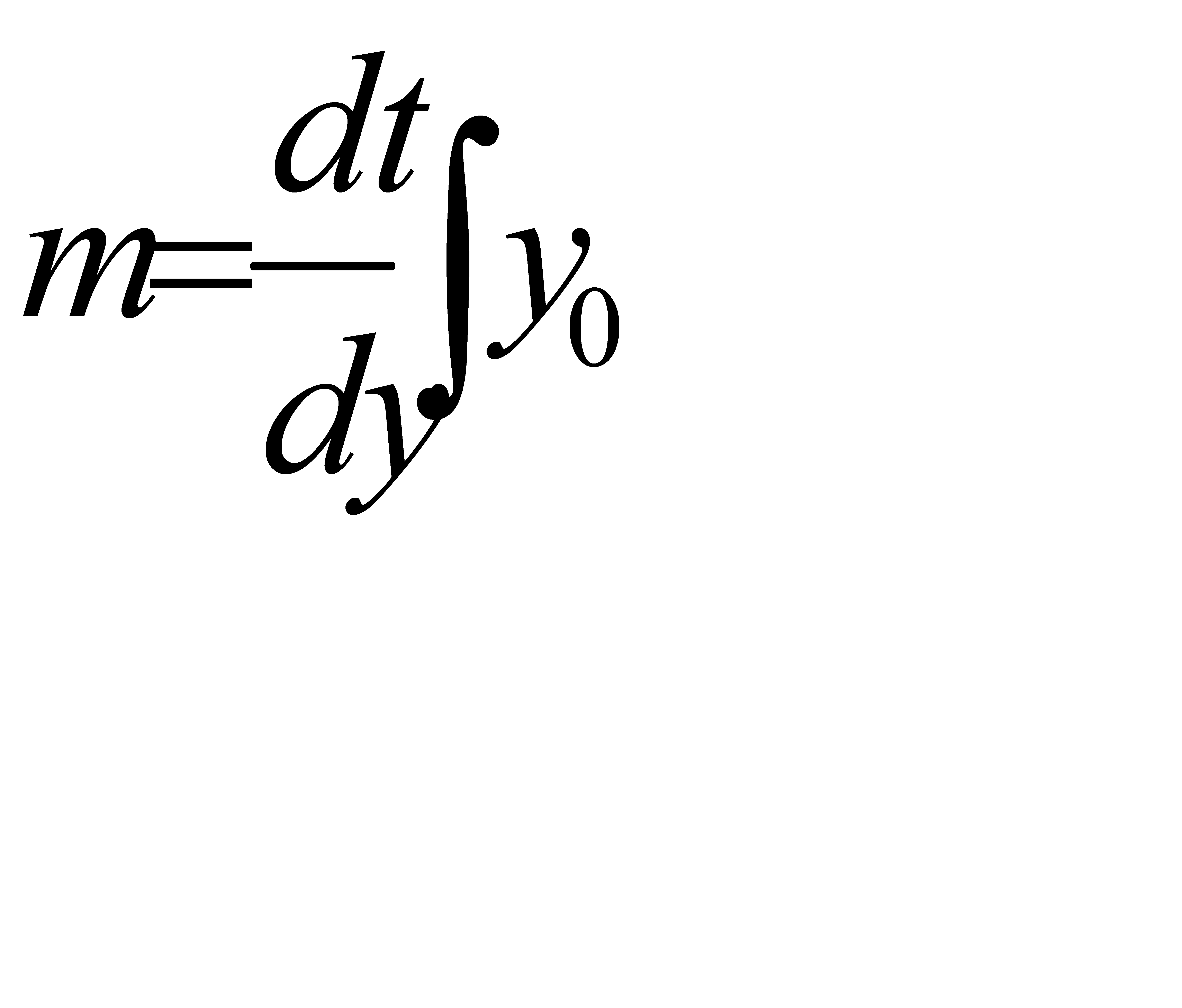
Следовательно 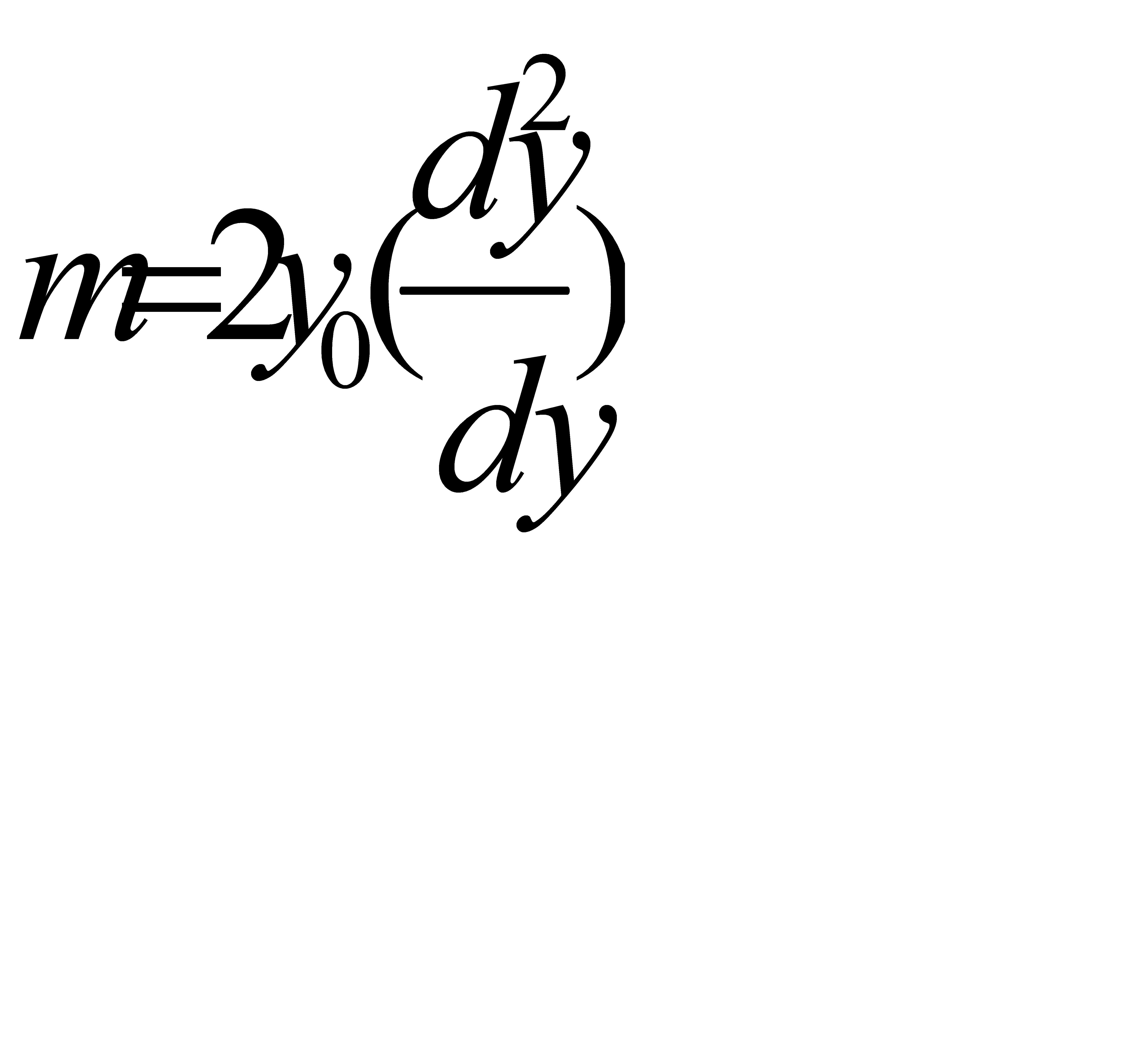
Пример:
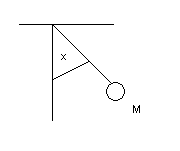 T=Mgsin
T=Mgsin 
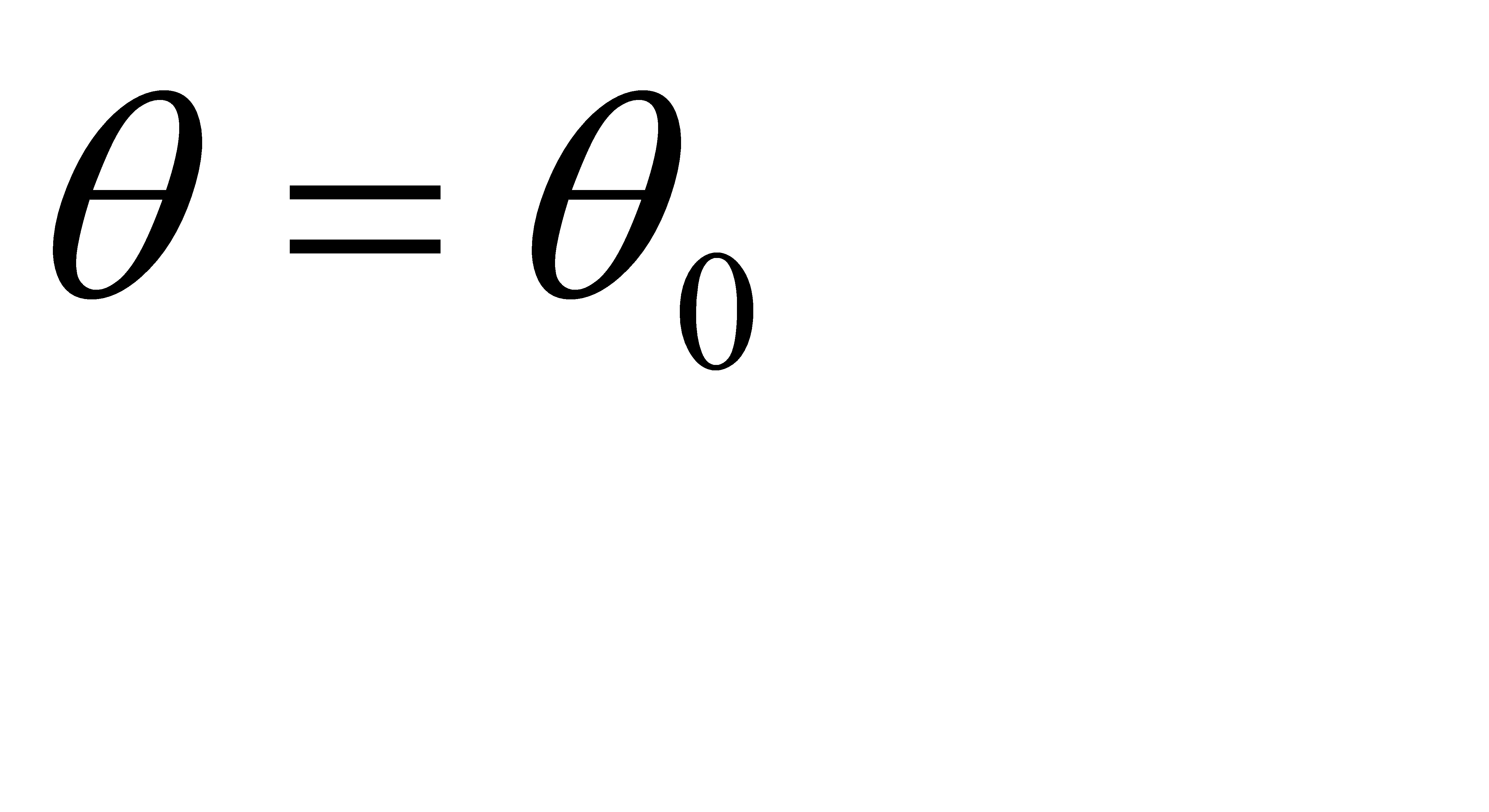
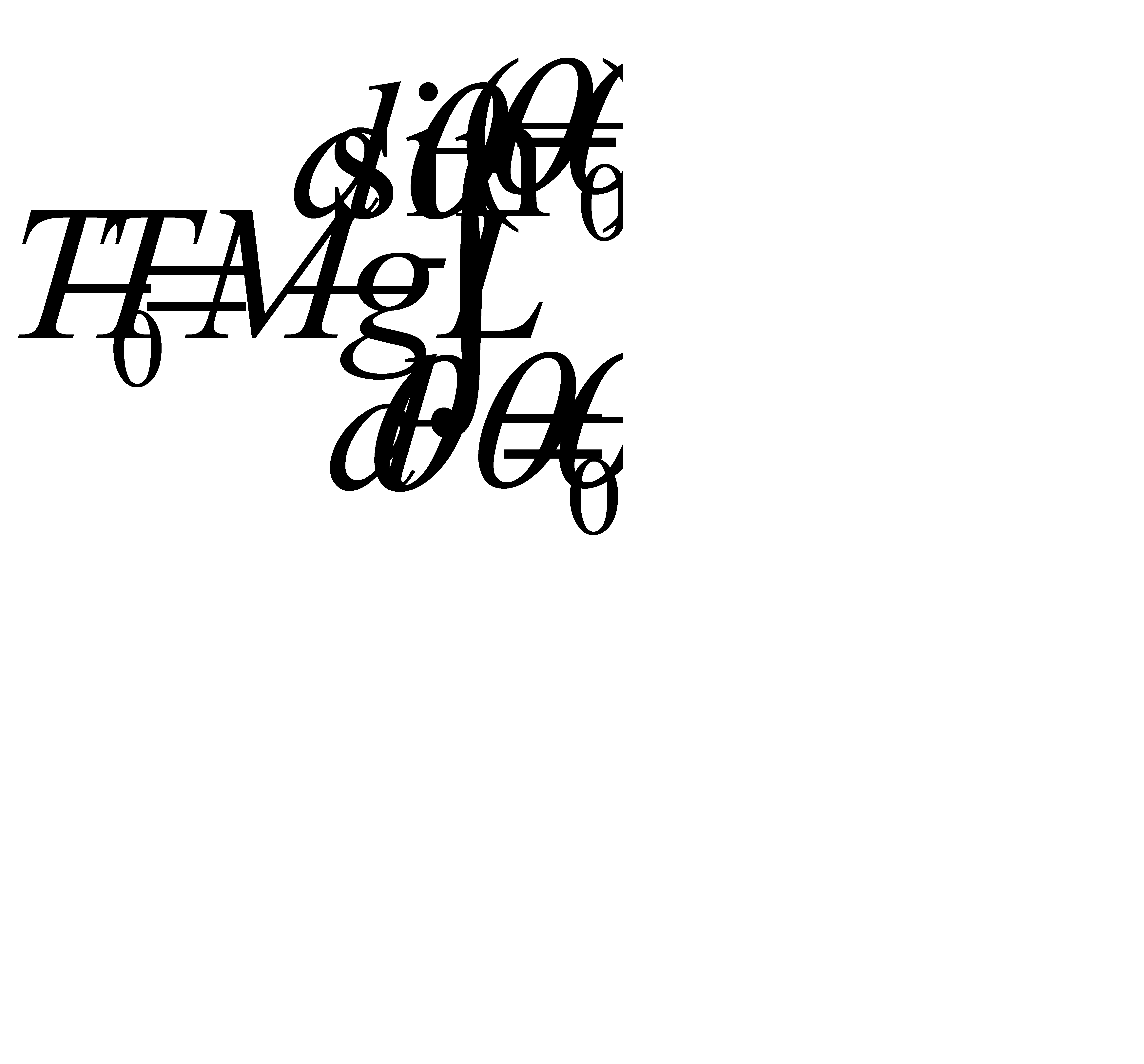
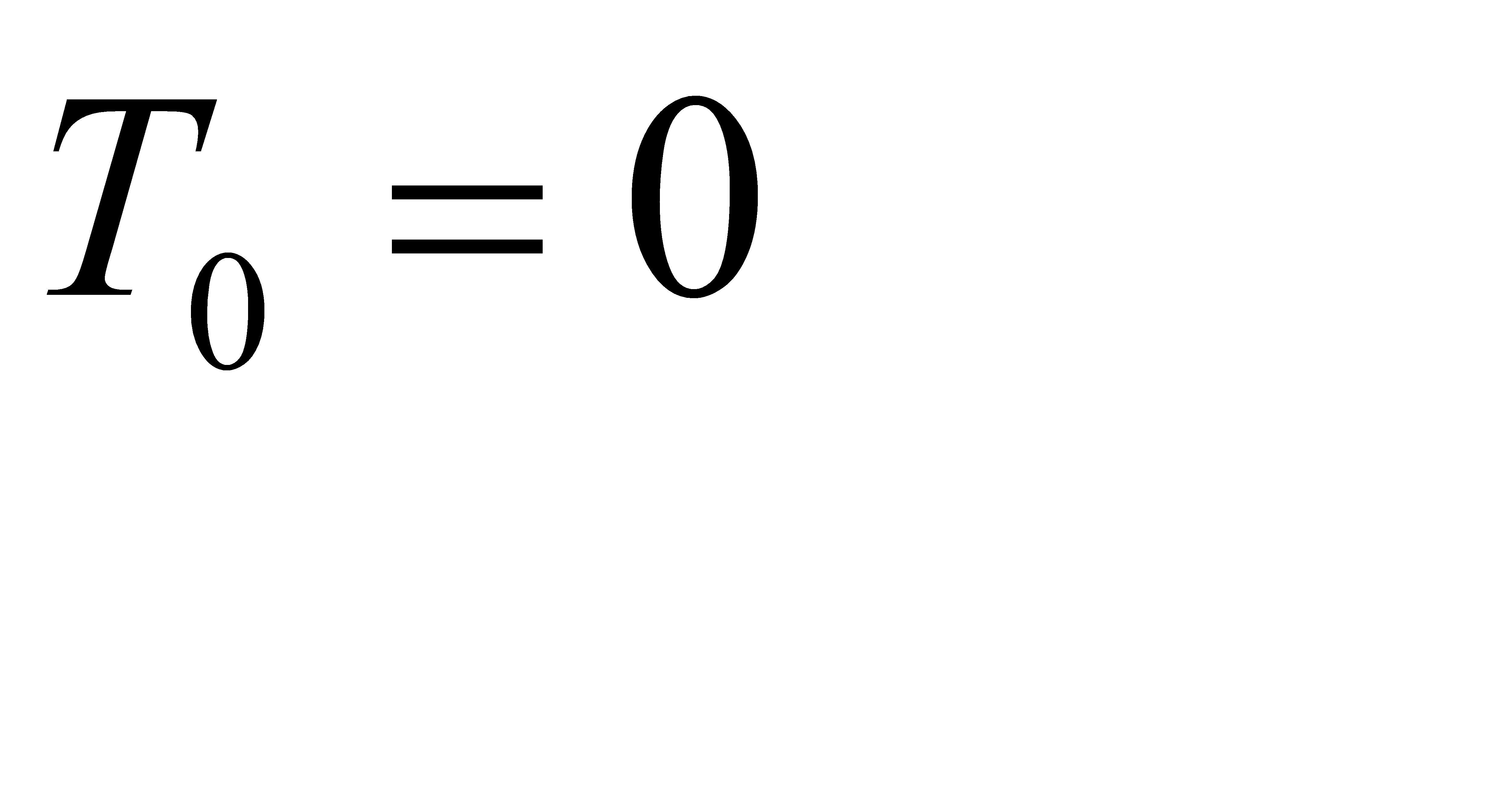

. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САУ
2.1. Передаточная функция
Целью рассмотрения САУ может быть решение одной из двух задач: задачи анализа или задачи синтеза. Но в любом случае порядок исследования САУ включает в себя следующие этапы: математическое описание, исследование установившихся режимов, исследование переходных режимов.
Рассмотрим случай, когда в замкнутой системе можно выделить объект О и управляющее устройство УУ, как показано на рис.2.1.
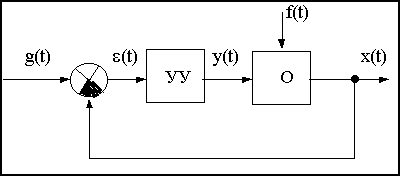
Рис.2.1
Общее уравнение САУ получается из системы уравнений объекта и управляющего устройства.
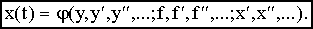
Состояние объекта характеризуется выходной величиной x(t), регулирующим воздействием y(t) и возмущением f(t). Тогда выходная величина может быть представлена функцией:
Состояние управляющего устройства характеризуется регулирующим воздействием y(t) и входным воздействием . Процессы в УУ будут описываться двумя уравнениями:
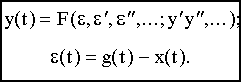
Три последних уравнения полностью описывают процессы в САУ. Если в этих уравнениях исключить переменные y(t) и , то получим дифференциальное уравнение САУ: 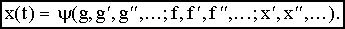
Это уравнение оценивает состояние системы во времени, определяет переходные процессы и обычно называется уравнением динамики.
Однако в форме дифференциальных уравнений математическое описание в теории автоматического управления обычно не применяется вследствие сложности решения таких уравнений.
Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления.
Возьмем некоторый элемент САУ, имеющий один вход и один выход. Дифференциальное уравнение элемента в общем случае имеет вид:
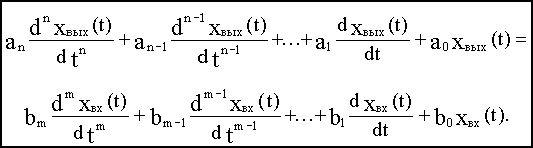
Если в уравнение (2.1) вместо функции времени xвых(t) и xвх(t) ввести функции Xвых(p) и Xвх(p) комплексного переменного р, поставив условием, что эти функции связаны зависимостями:
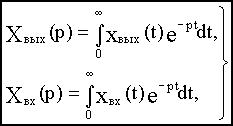 (2.2)
(2.2)
то оказывается, что дифференциальное уравнение, содержащее функции xвых(t) и xвх(t) при нулевых начальных условиях, равносильно линейному алгебраическому уравнению, содержащему функции Xвых(p) и Xвх(p):
anpnXвых(p)+an-1pn-1Xвых(p)+...+a1pXвых(p)+a0Xвых(p)=
=bmpmXвх(p)+bm-1pm-1Xвх(p)+...+b1pXвх(p)+b0Xвх(p).(2.3)
Такой переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называется преобразованием Лапласа.
Функция X(p) называется изображением функции x(t), функция x(t) называется оригиналом функции X(p).
Операция перехода от искомой функции x(t) к ее изображению X(p) (нахождение изображения от оригинала) называется прямым преобразованием Лапласа и записывается условно с помощью символа L как
L{x(t)}=X(p).
Операция перехода от изображения X(p) к искомой функции x(t) (нахождение оригинала по изображению) называется обратным преобразованием Лапласа и записывается условно с помощью символа L-1 как L-1{X(p)}=x(t).
Формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях получается путем замены символов дифференцирования оригиналов функций dn/dtn, dn-1/dtn-1...,d/dt соответственно на pn,pn-1,...p и функций x(t)- их изображениями X(p). С комплексной переменной p, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.
Так как возможность однозначного перехода от дифференциального уравнения к алгебраическому значительно упрощает расчеты, то важно убедиться в правомерности такого перехода. Обозначим в исходном дифференциальном уравнении 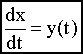 и согласно интегралу (2.2) найдем изображение:
и согласно интегралу (2.2) найдем изображение:
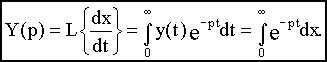
Согласно правилу интегрирования по частям
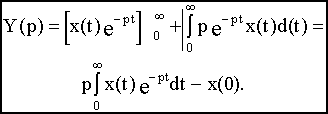
При нулевых начальных условиях x(0)=0 и с учетом (2.2) получим:
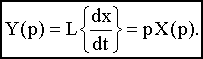
Таким образом, операция дифференцирования оригинала соответствует операции умножения изображения этого оригинала на комплексное число p.
Так как 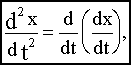 то
то 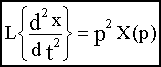 и т.д.
и т.д.
Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (2.1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.
Преобразование дифференциальных уравнений по Лапласу позволяет свести эту задачу к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение X(p) искомой функции x(t), определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.
Кроме того, преобразование дифференциального уравнения по Лапласу дает возможность ввести понятие передаточной функции.
Вынеся в уравнении (2.3) Xвых(p) и Xвх(p) за скобки, получим:
(anpn+an-1pn-1+...+a1p+a0)Xвых(p)=
=(bmpm+bm-1pm-1+...+b1p+b0)Xвх(p).
Определим из этого уравнения отношение изображения выходной величины к изображению входной: 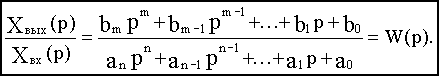 (2.4)
(2.4)
Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы).Передаточная функция W(p) является функцией комплексной переменной р: 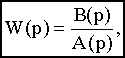
где A(p)=anpn+an-1pn-1+...+a1p+a0- полином степени n,
B(p)=bmpm+bm-1pm-1+...+b1p+b0- полином степени m.
Из определения передаточной функции следует, что:
Xвых(p)=Xвх(p)W(p).
Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.
Рассмотрим примеры по определению передаточной функций некоторых простейших схем, характерных для электроники.
Пример 1.
Вывести передаточную функцию для схемы на рис.2.2, считая входным воздействием приложенное напряжение u, а выходным - ток в цепи i.
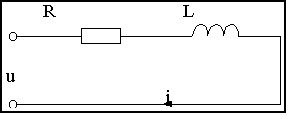
Рис.2.2
Процессы в схеме описываются уравнением:
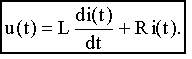
Перейдем к изображениям по Лапласу:
U(p)=LpI(p)+RI(p)=I(p)(Lp+1).
Составим передаточную функцию как отношение изображения выходной величины к изображению входной величины:
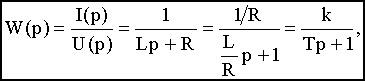
где k=1/R- коэффициент передачи,
T=L/R- постоянная времени.
Передаточные функции принято записывать в такой форме, чтобы свободные члены полиномов от р равнялись бы единице, что и сделано как в рассмотренном примере, так и в последующих.
Пример 2.
Вывести передаточную функцию схемы на рис.2.3, считая входной величиной напряжение u1, а выходной - u2.
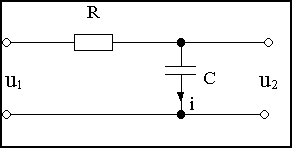
Рис.2.3
При выводе передаточной функции будем считать, что цепочка не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности) и сопротивление источника входного напряжения настолько велико, что его можно считать равным бесконечности.
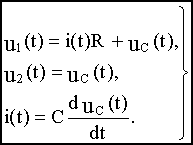 (а)(б)(в)
(а)(б)(в)
Подставим (в) в (а):
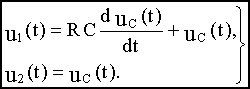
Перейдем к изображениям:
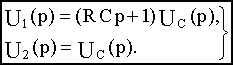
Передаточная функция
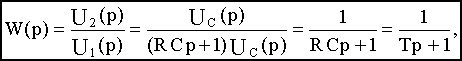
где T=RC- постоянная времени.
Пример 3
Вывести передаточную функцию схемы на рис.2.4, а , содержащей операционный усилитель.
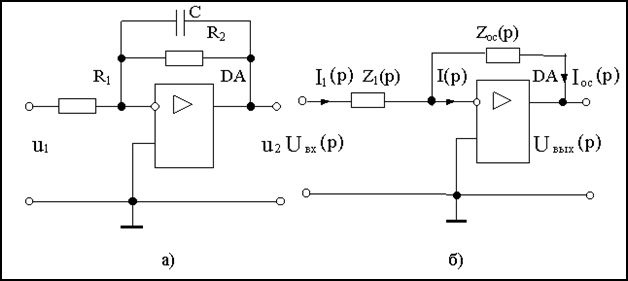
Рис.2.4
Операционными усилителями называются усилители постоянного тока малой мощности с большим коэффициентом усиления. В настоящее время они выполняются по интегральной технологии, т.е. в виде микросхем.
Выведем вначале передаточную функцию для типового включения операционного усилителя, показанного на рис.1, б, в общем виде.
Так как реальные микросхемы операционных усилителей имеют большой коэффициент усиления kоу и большое входное сопротивление rвх, то предположим, что 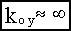 и
и 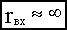 .
.
С учетом принятых допущений напряжение между инвертирующим и неинвертирующим входами операционного усилителя
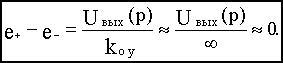
Отсюда следует, что напряжение на входе “-“ (инвертирующем) и тогда
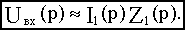
Кроме того, учитывая, что 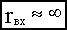 , можно считать
, можно считать 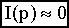 и, следовательно
и, следовательно

Выходное напряжение схемы тогда определяется следующим соотношением:

Теперь легко получить выражение для передаточной функции схемы (см.рис.1, б):
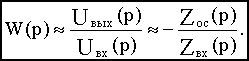
Знак “минус” в последнем выражении указывает на то, что полярность выходного напряжения схемы противоположна полярности входного напряжения.
Для определения передаточной функции схемы на рис.1, а вначале найдем сопротивление конденсатора ZC(p) в операторной форме.
Мгновенное значение тока через емкость равно:
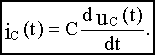
Переходя к изображениям по Лапласу:
IC(p)=CpUC(p).
Из последнего равенства
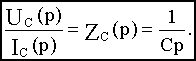
(Аналогично для индуктивности можно получить ZL(p)=Lp).
Используя выведенное значение ZC(p), для схемы на рис.2.6, а получим:
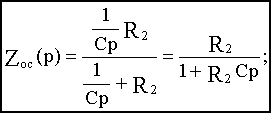
Z1(p)=R1;
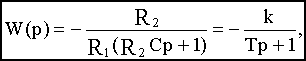
где k=R2/R1- коэффициент передачи,
T=R2C- постоянная времени.
2.2. Частотные характеристики
Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотной  , то после затухания переходных процессов на выходе также возникают синусоидальные колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как из
, то после затухания переходных процессов на выходе также возникают синусоидальные колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как из  вестно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как
вестно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как 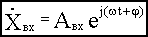 и
и 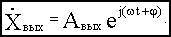
Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.
Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:
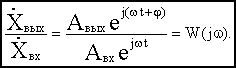 (2.6)
(2.6)
Функция 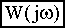 называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную :
называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную : 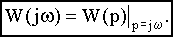 (2.7)
(2.7)
В различных формах записи функцию 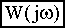 можно представить в следующем виде:
можно представить в следующем виде:
 (2.8)
(2.8)
где 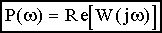 и
и 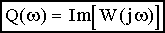 - действительная и мнимая части комплексной частотной функции,
- действительная и мнимая части комплексной частотной функции,  и - модуль и аргумент комплексной частотной функции
и - модуль и аргумент комплексной частотной функции 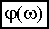 .
.
При фиксированном значении частоты комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.5.
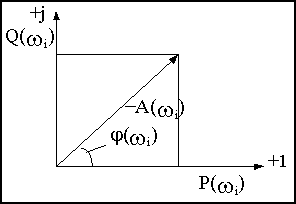
Рис.2.5
Изменение частоты приведет к изменению величины и расположения вектора на комплексной плоскости, а конец вектора опишет некоторую траекторию. Геометрическое место концов векторов комплексной частотной функции при изменении частоты от нуля до бесконечности называется амплитудно-фазовой частотной характеристикой (АФЧХ).
В свою очередь все величины, представленные в (2.8), являются соответствующими частотными функциями, а построенные по выражениям для функций графики - частотными характеристиками.
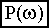 называется вещественной частотной, а
называется вещественной частотной, а  - мнимой частотной характеристикой.
- мнимой частотной характеристикой.
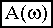 показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.
показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.
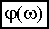 показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.
показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.
Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис.2.5.
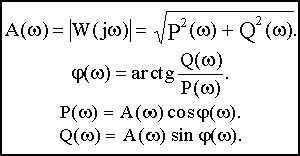 В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.
В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.
Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на входе Pвых к мощности на входе Pвх в технике принят бел. Так как мощность сигнала пропорциональна его амплитуде, получим:
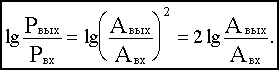
Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел 1дБ=0,1 Б.
С учетом этого можно записать: 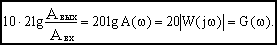
Величина логарифма амплитудной частотной характеристики, выраженная в децибелах называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ).
Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз - на 40 дБ, в 1000 раз - на 60 дБ и т.д.
Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.
1дБ=20lg(Aвых/Aвх);
lg(Aвых/Aвх)=1/20;
То есть 1 дБ 1,222.
2 дБ ~ (1,222)2=1,259;
3 дБ ~ (1,222)3=1,259;
4 дБ ~ 1,585;
5 дБ ~ 1,778;
6 дБ ~ 1,995 2.
Фазовая частотная характеристика 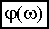 , построенная в полулогарифмическом масштабе (в координатах: угол в градусах или радианах и
, построенная в полулогарифмическом масштабе (в координатах: угол в градусах или радианах и  ), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).
), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).
За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.
В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную 
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке 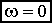 , так как
, так как 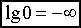 . Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.
. Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.
Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза  . Ось абсцисс соответствует значению
. Ось абсцисс соответствует значению 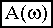 , то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).
, то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).
Из рассмотренных здесь частотных характеристик две можно получить экспериментально-амплитудную 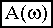 и фазовую
и фазовую 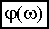 ). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например - по формуле (2.8). Кроме того, рассчитав по экспериментальным данным
). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например - по формуле (2.8). Кроме того, рассчитав по экспериментальным данным 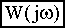 , по (2.7) путем обратной подстановки (заменив на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).
, по (2.7) путем обратной подстановки (заменив на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).
К содержанию
2.3. Временные функции и характеристики
Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы некоторого типового воздействия.
Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы некоторого типового воздействия.
Так как временные характеристики могут быть получены не только путем решения дифференциального уравнения, но и экспериментально, то возможность определения динамических свойств системы по временной характеристике имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение.
В качестве типовых воздействий наиболее широкое применение находят единичное ступенчатое и единичное импульсное воздействия.
Математическое выражение единичного ступенчатого воздействия может быть записано в виде
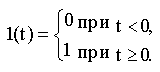
Под единичным импульсным воздействием понимается предельно короткий импульс 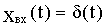
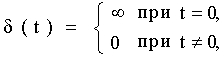
площадь которого равна единице, то есть
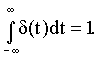
Выражение для единичного импульса в математике принято называть дельта-функцией 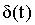 .
.
Графическое изображение реакции системы на единичное ступенчатое воздействие называется переходной характеристикой.
Аналитическое выражение переходной характеристики обозначается h(t) и называется переходной функцией.
Графическое изображение реакции системы на единичное импульсное воздействие называется импульсной переходной характеристикой.
Аналитическое выражение импульсной переходной характеристики обозначается и называется импульсной переходной функцией или весовой функцией (функцией веса).
При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс часто возникает при включениях и изменениях задающего воздействия.
При поступлении на вход системы с передаточной функцией W(p) величины xвх(t)=1(t) на выходе получаем переходную характеристику xвых(t)=h(t).
В преобразованном по Лапласу виде входная и выходная величины запишутся
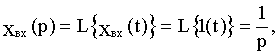
L{h(t)}=h(p)=xвых(p).
С учетом этих соотношений получим:
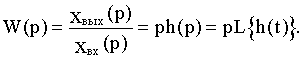 (2.9)
(2.9)
Из последнего выражения следует, что по переходной функции можно получить передаточную функцию.
При поступлении на вход САР величины 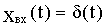 на выходе получаем импульсную переходную характеристику или в преобразованном по Лапласу виде:
на выходе получаем импульсную переходную характеристику или в преобразованном по Лапласу виде:
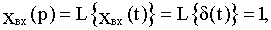
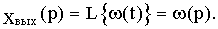
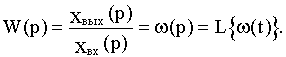
В результате определим:
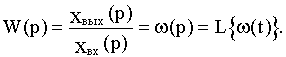
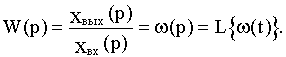 (2.10)
(2.10)
Установим связь между переходной и импульсной переходной функциями, приравняв правые части выражений (2.9) и (2.10):
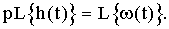
Но так как р соответствует символу дифференцирования, то
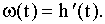
Импульсная переходная функция является производной от переходной функции.
2.4. Структурные схемы и их преобразование
В теории автоматического управления под структурной схемой понимается графическое изображение математического описания. То есть для составления структурной схемы система дробится на элементы, каждый из которых описывается простейшим математическим выражением ( в виде передаточной функции). Структурные схемы содержат следующие четыре типа элементов: звенья направленного действия; устройства сравнения, или сумматоры; линии связи; точки разветвления (узлы).
Звенья направленного действия изображаются прямоугольниками, внутри которых записываются их передаточные функции.
Между собой звенья соединяются с помощью линий связи. На этих линиях стрелками указывается направление распространения сигналов. Следует подчеркнуть, что в направлениях, противоположных указанным стрелками, сигналы не распространяются. Сами линии связи, также как и сумматоры, считаются идеальными, то есть никакими параметрами не обладают.
Сумматоры предназначены для суммирования сигналов (с учетом знака сигнала), как и на функциональных схемах.
Для распределения сигналов по различным направлениям используются узлы, которые обозначаются точками в местах пересечения линий связи.
Для удобства расчетов бывает необходимо преобразовать исходную структурную схему системы к какому-либо желаемому виду, чаще всего - к цепи последовательно соединенных звеньев. В связи с этим рассмотрим основные правила преобразования структурных схем.
При последовательном соединении n звеньев с передаточными функциями Wi(p) эквивалентная передаточная функция Wэ(p) определяется их произведением:
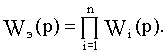
При параллельном соединении n звеньев эквивалентная передаточная функция определяется суммой передаточных функций Wi(p) отдельных звеньев:
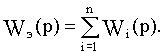
Для случая обратной связи при выводе эквивалентной передаточной функции замкнутого участка Wз(p) используем обозначения, приведенные на рис.2.6.
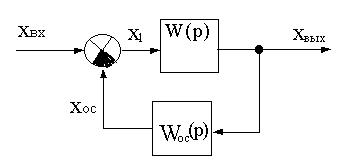
Рис.2.6 Схема замкнутого участка системы
Обратная связь называется отрицательной, если x1=xвх-xoc, как показано на схеме, и положительно, если x1=xвх+xoc.
Отсюда получаем передаточную функцию
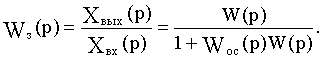
Для положительной обратной связи в знаменателе формулы знак "плюс" меняется на "минус".
Указанные три вида преобразования структурных схем являются наиболее часто встречающимися. Для остальных случаев сформулируем основной принцип преобразования и поясним несколькими примерами. При преобразовании структурной схемы передача сигнала по выбранному направлению не должна меняться.
Например, в структурной схеме на рис.2.7, а необходимо перенести узел через звено с передаточной функцией W2(p). Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией 1/W2(p), как показано на рис.2.7, б.
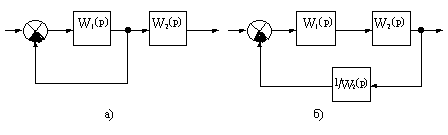
Рис.2.7 Преобразование структурной схемы
Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией 1/W2(p), как показано на рис.2.7, б.
В более сложных случаях в процессе преобразования необходимо производить определенные расчеты.
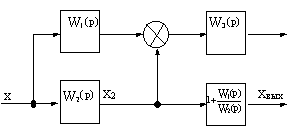
Например, в схеме на рис.2.8, а узел 1 необходимо перенести на выход звена с передаточной функцией W2(p).
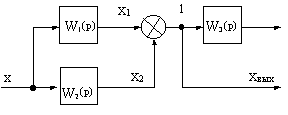
а) б)
Рис.2.8 Преобразование структурной схемы
Установим связь между величинами Xвых(p) и X2(p).
На входе звеньев с передаточными функциями W1(p) и W2(p) действует сигнал
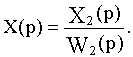
На выходе звена с передаточной функцией W1(p)
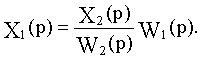
На выходе сумматора в узле 1
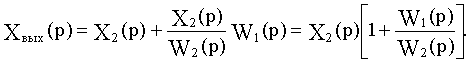
Отсюда видно, что в рассматриваемом примере при переносе узла необходимо ввести фиктивное звено с передаточной функцией , как показано на рис. 2.10, б.
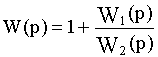
При переносе узла в схеме на рис.2.9, а с выхода сумматора на его положительный вход найдем передаточную функцию фиктивного звена без дополнительных пояснений.
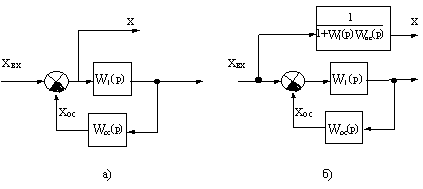
Рис.2.9
2.5. Типовые звенья и их характеристики
Известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.
Все линейные типовые звенья разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие. Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания - характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.
В звеньях, относящихся к группе интегрирующих, при постоянном входном воздействии выходная величина неограниченно растет.
Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.
Рассмотрим типовые звенья и их характеристики.
Пропорциональное (безинерционное) звено. Описывается уравнением и имеет передаточную функцию
xвых(t)=kxвх(t), W(p)=k.
Параметр k называется в общем случае коэффициентом передачи звена и может иметь любую размерность. В частных случаях, когда k является величиной безразмерной, принято пользоваться термином "коэффициент усиления".
Частные и временные функции звена:
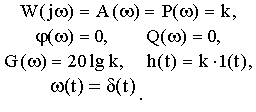
Примерами таких звеньев могут служить механические связи, электронные усилители сигналов на низких частотах и др.
Апериодическое звено 1ого порядка описывается ДУ следующего вида:
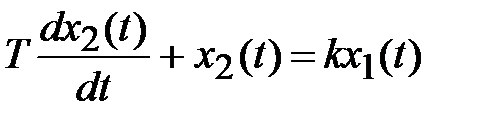 или
или 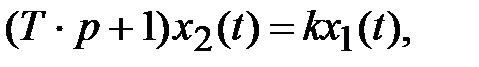
где 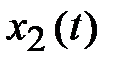 – выходная величина;
– выходная величина; 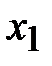 (t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
(t) – входная величина; Т─ постоянная времени звена; k─ коэффициент передачи.
Передаточная функция
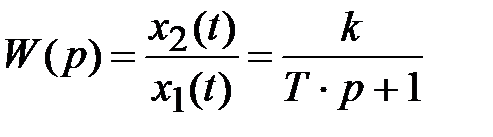 ;
;
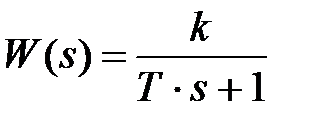 ,
,
где  ;
;  .
.
К этим звеньям относятся исполнительные двигатели, усилители мощности, магнитные усилители , RC – фильтры.
АЧХ звена определяется выражением:

где  – сопрягающая частота.
– сопрягающая частота.
ФЧХ звена: 
Переходная характеристика:

Весовая функция

Графическое изображение переходной и весовой функции (рис. 3):

|

|

|

|

|

|

|

|
Рис. 3. Переходная и весовая характеристики апериодического звена