Лекция.
Қажетті және жеткілікті шарттар
Теореманың қажетті және жеткілікті шарттары
Мектеп математика курсында “қажетті шарт”, “жеткілікті шарт”, “қажетті және жеткілікті шарт” ұғымдары оқушылардың логикалық ойлауын жетілдіруде, теоремаларды дәлелдеуде және көптеген есептер шығару процесінде кең түрде қолданылады.
Егер А қасиетінің орындалуынан В қасиетінің орындалуы келіп шықса, онда А қасиет В қасиетінің бар болуы үшін жеткілікті шарт болады. Мысалы, “Егер екі қосылғыштың әрқайсысы қандай да бір санға бөлінсе, онда олардың қосындысы да сол санға бөлінеді” деген пайымды былайша тұжырымдауға болады: “Екі қосылғыштың қосындысы қандай да бір санға бөлінуі үшін әрбір қосылғыш сол санға бөлінуі жеткілікті”.
Егер А қасиет орындалмағанда, В қасиет те орындалмаса, онда А қасиет В қасиетінің бар болуы үшін қажетті шарт болады.
Егер А-ның орындалуы В қасиетінің бар болуына алып келсе және А орындалмағанда В-ның орындалуы мүмкін емес болса, онда А қасиет В қасиетінің бар болуы үшін қажетті және жеткілікті шарт болады.
Сонымен қандай теорема болмасын оның шарты қорытындысы үшін жеткілікті, ал қорытындысы шарты үшін қажетті шарт болады. Қысқартып айтқанда А-ның В үшін жеткілікті, ал В-ның А үшін қажетті шарты екенін байқаймыз.
Қажетті және жеткілікті шарттың өзі, тура теорема мен оған кері теореманың дұрыстығын көрсетеді. Сондай-ақ, керісінше, тура және кері теоремалардың дұрыстығы қажетті және жеткілікті шарттарды тағайындауға мүмкіндік береді.
“Қажетті және жеткілікті” сөзі көпшілік жағдайда “сонда, тек сонда ғана”, “сонда, тек сонда”, “сонда ғана”, “тек қана” т.б. сөздерінің бірімен ауыстырылады.
Қажетті және жеткілікті шарт туралы мынадай теореманы дәлелдейік.
Теорема.  кесіндісін де анықталған және үздіксіз
кесіндісін де анықталған және үздіксіз  функциясының
функциясының  анықталған интегралы бар болуы үшін
анықталған интегралы бар болуы үшін  шартының орындалуы қажетті және жеткілікті.
шартының орындалуы қажетті және жеткілікті.
Қажеттілігінің дәлелдемесі. 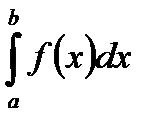 -анықталған интегралы бар болғанда
-анықталған интегралы бар болғанда екенін дәлелдейміз. Анықталған интегралдың бар болуы үшін, анықтамасына сәйкес
екенін дәлелдейміз. Анықталған интегралдың бар болуы үшін, анықтамасына сәйкес  болады. Шектің анықтамасы бойынша.
болады. Шектің анықтамасы бойынша.
 немесе
немесе  (1)
(1)
Бізге, G – интегралдық қосынды Дарбудың төменгі және жоғарғы қосындыларының арасында жататындығы белгілі, сондықтан
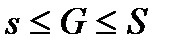 (2)
(2)
болады (1) мен (2)-ні біріктіріп, төмендегі теңсіздікті құрамыз:
 (3)
(3)
(3) теңсіздіктен төмендегі теңсіздіктерді бөліп алуға болады:

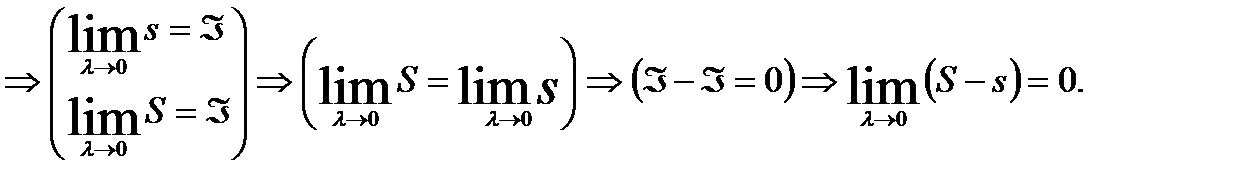
Теореманың қажеттілігінің дұрыстығы дәлелденді.
Жеткілікті шартының дәлелдемесі
 болғанда
болғанда  интегралының бар болатындығын көрсетейік. Ол үшін
интегралының бар болатындығын көрсетейік. Ол үшін  да G интегралдың қосындысының шегі
да G интегралдың қосындысының шегі 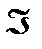 -ге ие болатындығын көрсету жеткілікті.
-ге ие болатындығын көрсету жеткілікті.
Бізге Дарбудың төменгі қосындысының монотон өсетіндігі және жоғарыдан шектелгендігі және ол өзінің дәл жоғарғы шекарасына ие болатындығы белгілі:

Сондай-ақ, Дарбудың жоғарғы қосындысының төменгі дәл шекарасына ие болатындығы белгілі:
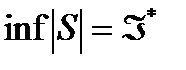 .
.
Төменгі және жоғарғы шекаралардың анықтамасы бойынша  және
және  болады. Осы екі теңсіздікті біріктірсек:
болады. Осы екі теңсіздікті біріктірсек:
 (1)
(1)
Бірақ  болғандықтан
болғандықтан  .
.
 (2)
(2)
(2)-ге сәйкес (1)-ні былайша жазуға болады:
 (3)
(3)
Бізге  екені белгілі, бұдан басқа
екені белгілі, бұдан басқа  (4)
(4)
болғандықтан (3) мен (4)-ге сәйкес:  болады.
болады.
Сонымен теореманың жеткілікті шартының дұрыстығы ды дәлелденді.
Сұрақтар:
1.Теореманың қажетті шарты;
2. Теореманың жеткілікті шарты;
3. Теореманың қажетті және жеткілікті шарты.
Пайданылған әдебиеттер
1.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж
2. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж
3. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003