Замечания 2.2.

1.Продолжение исследований, которое требуется в ряде случаев, разобранных в табл. 2.1, при решении практических задач, как правило, не проводится, за исключением небольшого числа модельных примеров.

2. Если требуется определить глобальные экстремумы, то они находятся в результате сравнения значений функции в точках локальных минимумов и максимумов с учетом ограниченности функции на Rn .

3. Для случая функции f ( x ) одной переменной ( n = 1) можно сформулировать правило, заменяющее п. 2 алгоритма:

Если функция f ( x ) и ее производные непрерывны, то точка х* является точкой экстремума тогда и только тогда, когда число т — четное, где т — порядок первой не обращающейся в нуль в точке х * производной. Если f ( m ) ( x *) > 0, то в точке х* — локальный минимум, а если f ( m ) ( x *) < 0, то в точке х* — локальный максимум. Если число т нечетное, в точке х * нет экстремума.

4. Часто на практике, особенно при применении численных методов поиска экстремума ... требуется проверить, выполняются ли необходимые и достаточные условия экстремума в некоторой точке. Такой анализ необходим, так как многие численные методы позволяют найти лишь стационарную точку, тип которой требует уточнения.

Рис. 2.1

Пример 2.1.Найти экстремум функции на множестве R 2 .

1. Запишем необходимые условия экстремума первого порядка:

В результате решения системы получаем стационарную точку х * = (0, 0) T .

 

Таблица 2.1

Критерии проверки достаточных и необходимых условий второго порядка
в задаче поиска безусловного экстремума

2. Проверим выполнение достаточных условий экстремума.

Первый способ . Матрица Гессе имеет вид 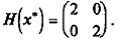Так как то в точке x * локальный минимум (строк 1 в табл. 2.1).

Второй способ . Найдем собственные значения матрицы Гессе, используя (2.10):

Отсюда (2 – λ)2 = 0 и λ1 = λ2 = 2 > 0. Так как все собственные значения положительны, то в точке х * локальный минимум (строка 1 в табл. 2.1). Следовательно, функция является строго выпуклой на множестве R 2 . Поэтому точка локального минимума является и точкой глобального минимума (см. п. 3 утверждения 1.1).

3. Вычислим значение функции в точке глобального минимума: f ( x *) = 0.

< > Необходимые и достаточные условия условного максимума