Билет 17

1. Кинетическая и потенциальная энергия. Потенциальная энергия тела, поднятого над Землёй. Потенциальная энергия деформированной пружины. Вторая космическая скорость.

 

 

Кинетическая энергия- работа, которую может совершить система за счет остановки всех своих частей.

Кинетическая энергия вращательного движения:

Кинетическая энергия поступательного движения:

Как вывести кинетическую энергию поступательного движения:

Как вывести кинетическую энергию вращательного движения:

Теоре́ма Кёнига:

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где — полная кинетическая энергия системы, — кинетическая энергия движения центра масс, — относительная кинетическая энергия системы.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Потенциальная энергия - работа, которую может совершить система за счет изменения своей конфигурации (взаимного расположения тел системы).

Потенциальные силы - силы, работа которых не зависит от скорости и траектории, но зависит от координаты. Сила тяжести, сила упругости.

Консервативные силы - потенциальные силы, работы которых не зависит от времени.

Работа потенциальной силы на замкнутой траектории равна 0.

Потенциальная энергия тела в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

Как вывести потенциальную энергию тела, поднятого над Землёй:

Энергия упругой деформации:

Как вывести потенциальную энергию упругой деформации:

ВАЖНО: Работа консервативной силы равна изменению потенциальной энергии, взятому с противоположным знаком.

Про трение:

Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.

Запишем затем закон сохранения энергии

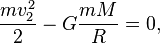
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v — вторая космическая скорость.

Решая это уравнение относительно v₂, получим

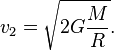
Между первой и второй космическими скоростями существует простое соотношение:

Для Земли вторая космическая скорость равна 11,2 км/с.