Билет 8

1. Закон всемирного тяготения. Гравитационная постоянная и методы её измерения. Гравитационная масса. Ускорение свободного падения, сила тяжести. Вес тела, невесомость и перегрузки.

 

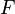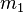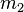Класси́ческая тео́рия тяготе́ния Ньютона (Зако́н всемирного тяготе́ния Ньютона) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном около 1666 года. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

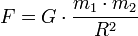
Здесь — гравитационная постоянная, равная 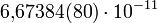м³/(кг с²).

 

Измеряли по-разному.

Опыт Кавендиша 1788:

l

На нити прикреплено зеркало и висит рейка с двумя шариками на концах. Подносят другие шары, маленькие отклоняются, нить поворачивается , зеркало поворачивается, луч направленный на зеркало отклоняется на угол, противолежащий катет которого может быть очень велик и очень точно измерен.

Или

Возьмём третий закон Кеплера

 

 

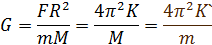
Как найти массу планеты:

Гравитационная масса - мера гравитационного взаимодействия тел.

Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.

Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.

Сила тяжести, действующая на любую материальную частицу, находящуюся вблизи земной поверхности, сила Р, определяемая как геометрическая сумма силы притяжения Земли F и центробежной (переносной) силы инерции Q учитывающей эффект суточного вращения Земли.

Ускоре́ние свобо́дного паде́ния — ускорение, придаваемое телу силой тяжести при исключении из рассмотрения других сил. Сила тяжести складывается из гравитационного притяжения планеты (или другого астрономического тела) и центробежной силы, вызванной суточным вращением планеты.

 

Центробежное ускорение является следствием вращения Земли вокруг своей оси, из-за чего связанные с Землёй системы отчёта не являются инерциальными. В точке, находящейся на расстоянии a от оси вращения, центробежное ускорение равно ω²a, где ω — угловая скорость вращения Земли, определяемая выражением ω = 2π/T, в котором Т — время одного оборота (звёздные сутки), равное для Земли 86164,1 секунды. Центробежное ускорение направлено от оси вращения. Можно подсчитать, что на Земле оно меняется от 0 на полюсах до 3,4 см/с² на экваторе, причём почти везде (кроме экватора) оно не сонаправлено с гравитационным ускорением, которое направлено к центру Земли.

 

В соответствии с законом всемирного тяготения, значение гравитационного ускорения на поверхности Земли или другой планеты можно связать с массой планеты M следующим соотношением:

,

где G — гравитационная постоянная (6,6742·10⁻¹¹ м³с⁻²кг⁻¹), а r — радиус планеты. Это соотношение справедливо в предположении, что планета является однородным шаром. Приведённое соотношение позволяет определить массу любой планеты, включая Землю, зная её радиус и гравитационное ускорение на её поверхности. Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.

Гравитационное ускорения на высоте h над поверхностью Земли (или другой планеты) можно вычислить по формуле:

,

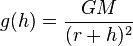где M - масса планеты.

Вес тела - сила, с которой тело действует на горизонтальную опору или вертикальных подвес.

Перегрузка - состояние тела, когда модуль веса превышает модуль силы тяжести, отношение абсолютное величины ускорения вызванного не гравитационными силами к ускорению свободного падения на поверхности Земли, перегрузка в 1 равна весу тела, перегрузка в 0 испытывается телом в свободном падении без других сил.

Невесомость - состояние тела, при котором его ускорение векторно равно ускорению свободного падения, перегрузка равна 0.