Билет 2

1. Радиус-вектор, его проекции. Вектор перемещения, траектория, путь, закон движения. Принцип независимости движения. Средняя и мгновенная скорости. Сложение скоростей. Прямолинейное равномерное движение.

Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Проекциями радиус-векторана Ох и Оу являются координаты конца этого вектора, rx, ry и rz. Проекция может быть положительной и отрицательной. Координаты вектора определяют его модуль. Модуль = корень из суммы квадратов проекций.

Перемеще́ние (в кинематике) —изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Можно определить перемещение, как изменение радиус-вектора точки: . Вектор перемещения имеет компоненты...

Траектория материа́льной то́чки — линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.

Путь — длина участка траектории материальной точки.

Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.

В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида

Можно записать в векторном виде для радиус-вектора.

Принцип независимости движений: если тело участвует одновременно в нескольких движениях, то каждое из этих движений происходит независимо от других.

Средняя скорость - векторная физическая величина, сонаправленная с перемещением и равная отношению изменения координаты точки к интервалы времени, за которое это перемещение было совершено.

 

Средняя путевая скорость (средний модуль скорости) — скалярная физическая величина, характеризующая отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено, предел, к которому стремится вектор средней скорости при .

Более строго:

.

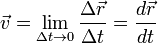Это производная радиус-вектора по времени. Направлена по касательной к траектории в сторону движения.

При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, которая движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.

В классической механике абсолютная скорость точки равна векторной сумме

её относительной и переносной скоростей:

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.

Простым языком:

Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

Равномерное прямолинейное движение — механическое движение, при котором мгновенная скорость тела в любой момент времени постоянна по величине и направлению.

Расстояние, пройденное точкой за время , задаётся в этом случае формулой .

Равномерное прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.

.

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной:

,

где — начальная координата точки, — проекция вектора скорости на координатную ось.