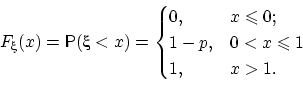Бернуллиевское распределение.

Ближайшим обобщением равномерного распределения является распределение Бернулли или бернуллиевское распределение, при котором нули и единицы возникают независимо с вероятностью p для единицы(событие А произойдет) и вероятностью q=1-p для нуля(событие А не произойдет); это число р принято называть параметром бернуллиевского распределения.

ИСПЫТАНИЕ ПРОВОДИТСЯ 1 РАЗ!

Говорят, что случайная величина А имеет распределение Бернулли с параметром p, если А принимает значения 1 и 0 с вероятностями p и q=1-p соответственно. Случайная величина А с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p: ни одного успеха или один успех. Таблица распределения А имеет вид:

А	0: не-А	1: А
Р	q	p

 

Функция распределения случайной величины ᶓ такова: