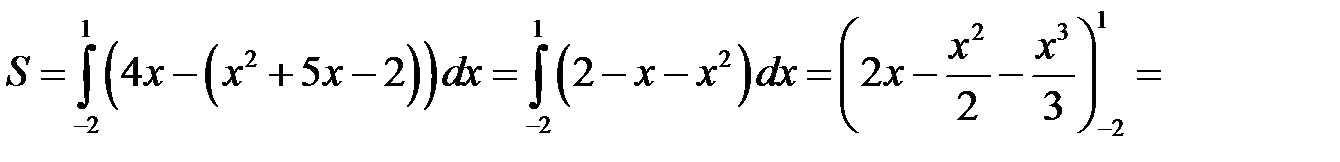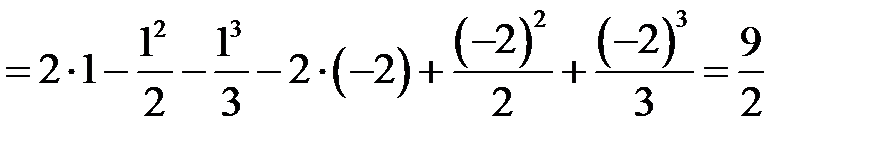Вычислить площадь фигуры, ограниченной линиями

Найти производные заданных функций

 

а)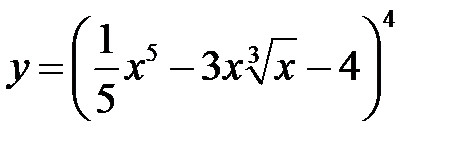

 

 

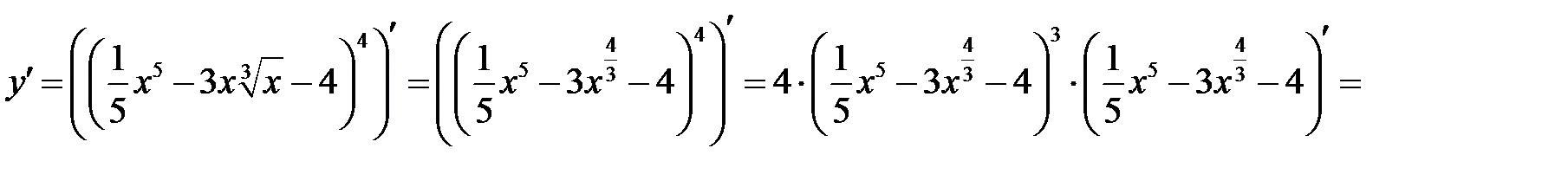
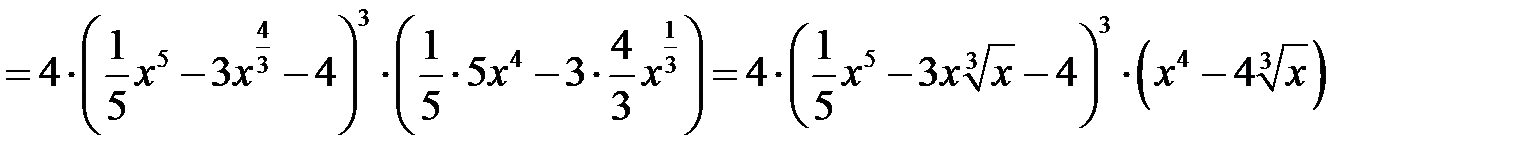
б)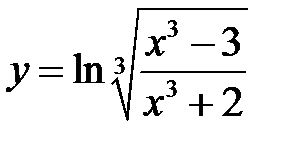

 

 

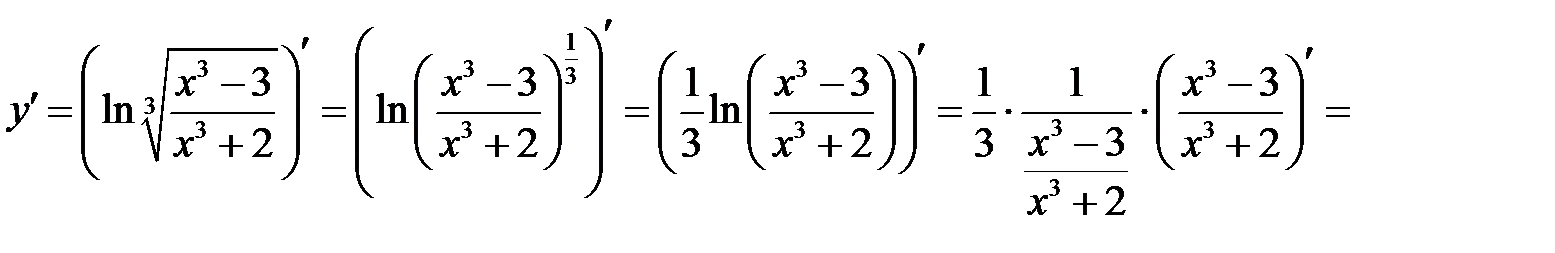
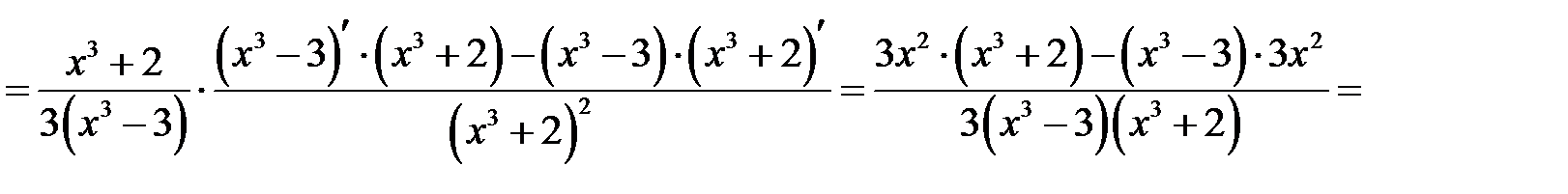
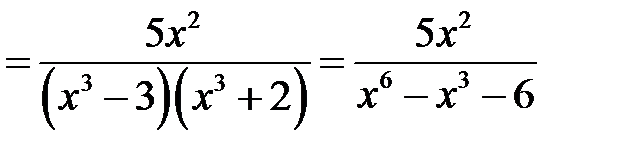
в)

 

 

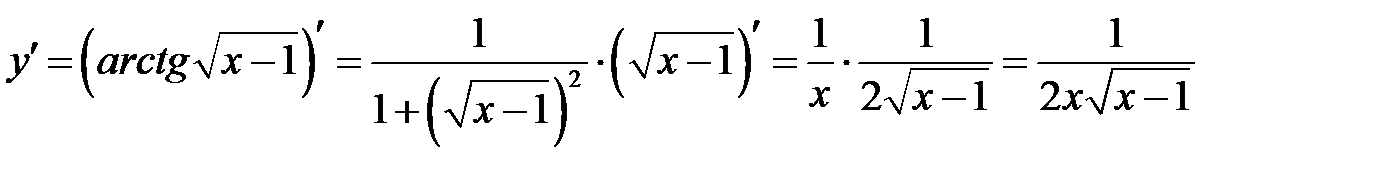
г)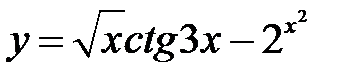

 

 

 

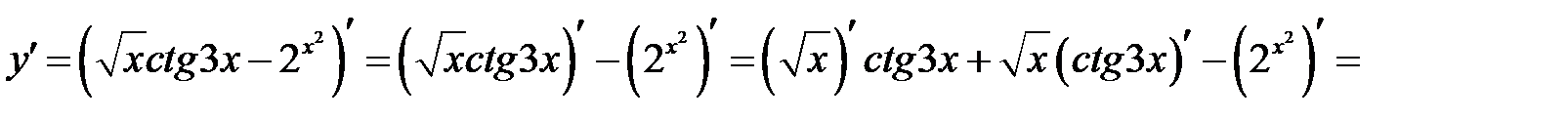
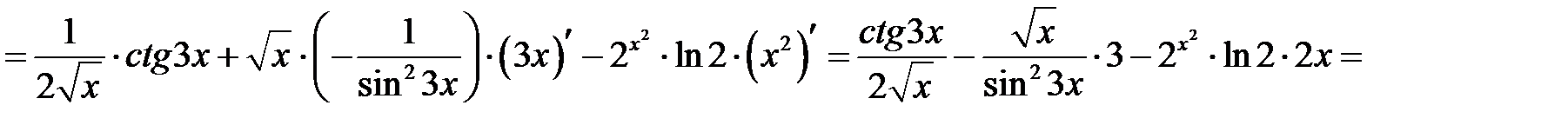
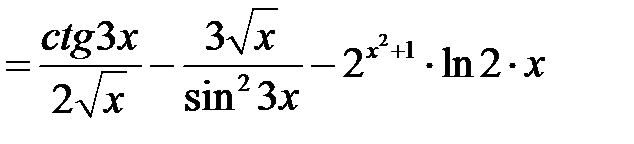
Провести полное исследование функции и построить ее график

 

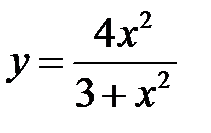
1) Область определения: 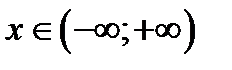, область значений: .

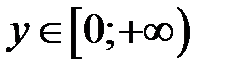2) Функция четная, т.к.

 

.

 

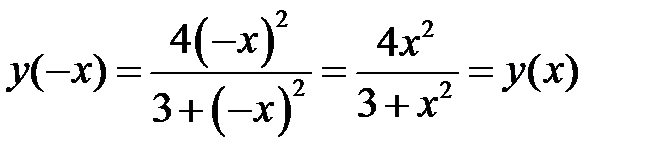Следовательно, имеется симметрия относительно начала координат.

3) Функция не периодическая.

4) Пересечение с осями:

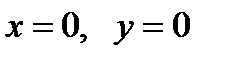
5) Функция не имеет разрывов.

6) Находим точки экстремума функции:

 

 

 

 

 

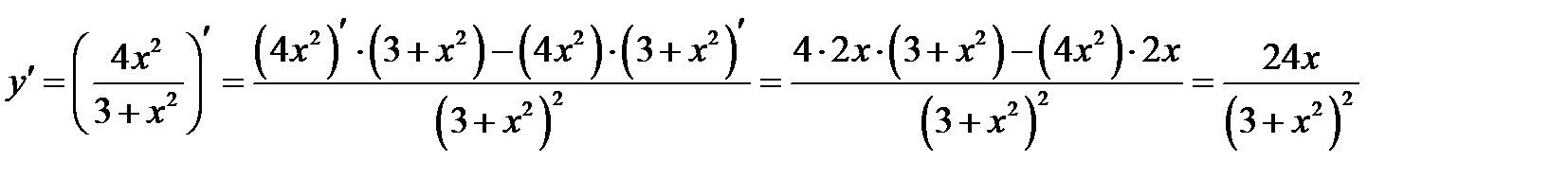
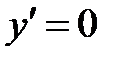
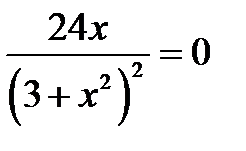
Составим таблицу:

x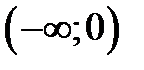
	-		+
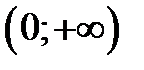
	убывает		возрастает

 

 

7) Находим точки перегиба функции:

 

 

 

 

 

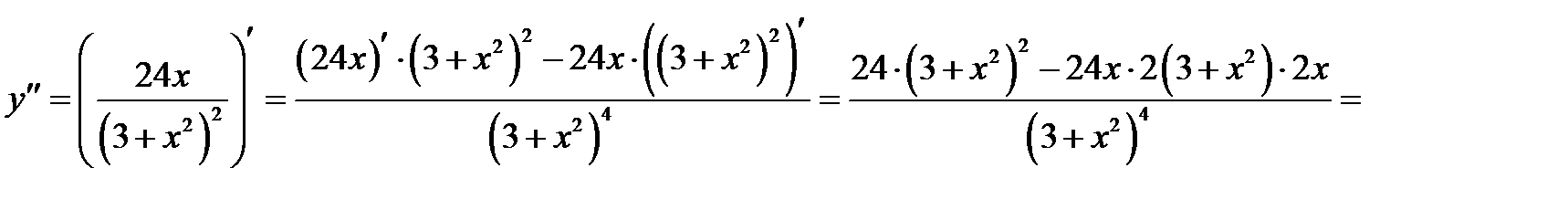
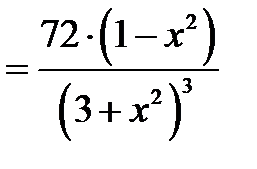
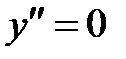
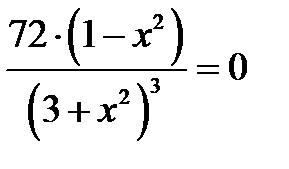
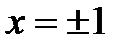
Составим таблицу:

x		-1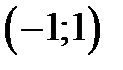
	-		+		-
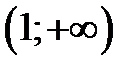
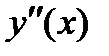
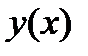
	Выпукла вверх		Выпукла вниз		Выпукла вверх

 

8) Асимптоты:

Ищем горизонтальные асимптоты:

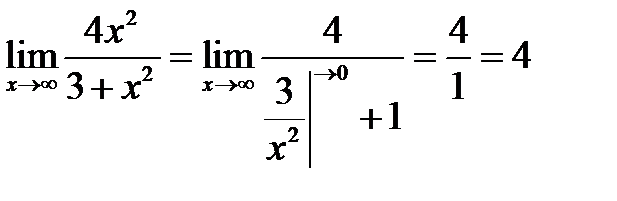
Получили горизонтальную асимптоту y=4.

 

9) Строим чертеж:

 

 

Найти неопределенные интегралы. Правильность полученных результатов проверить дифференцированием

 

а)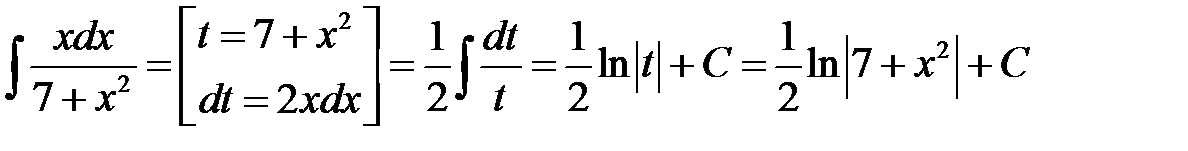

 

 

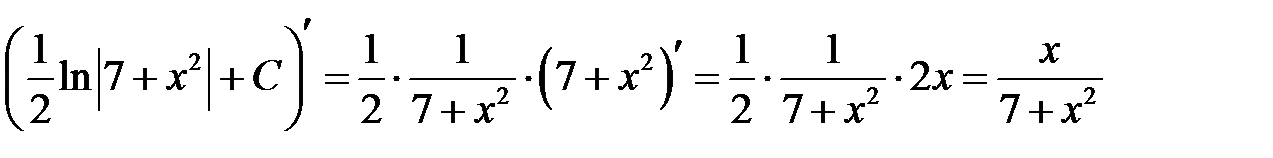
б)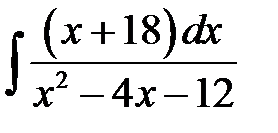

 

 

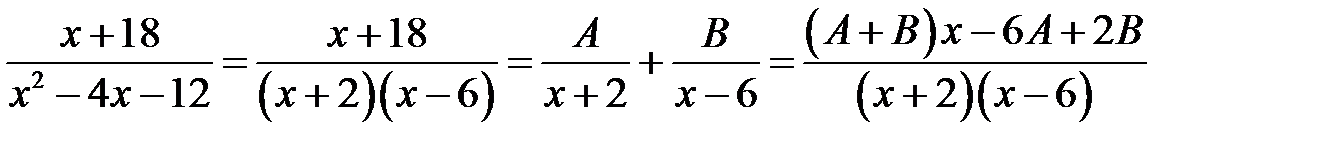
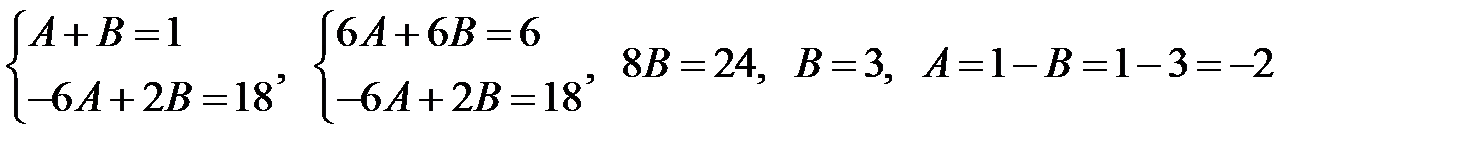
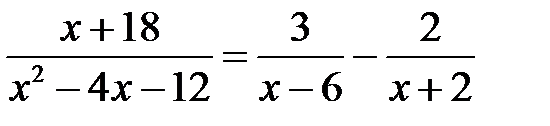
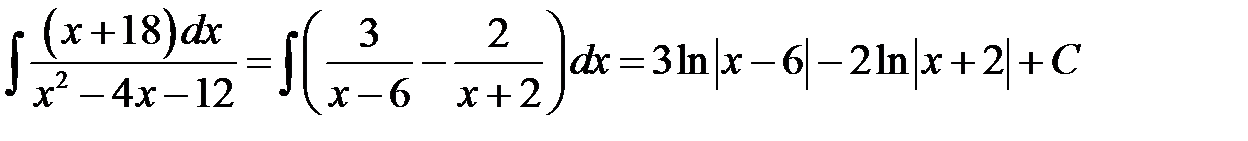
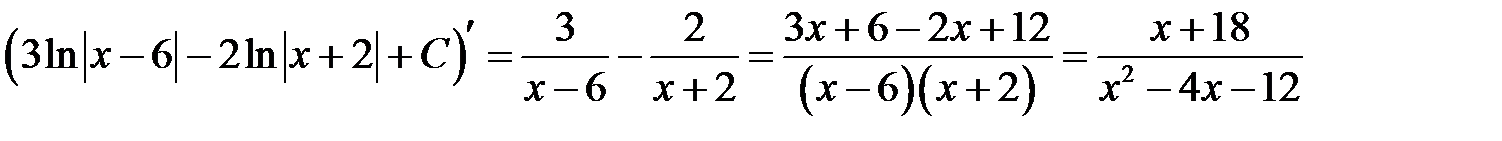
в)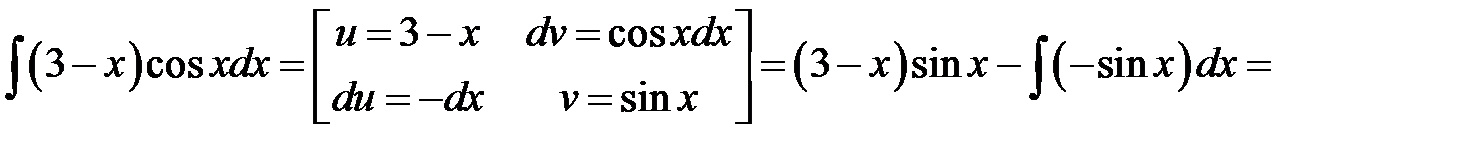

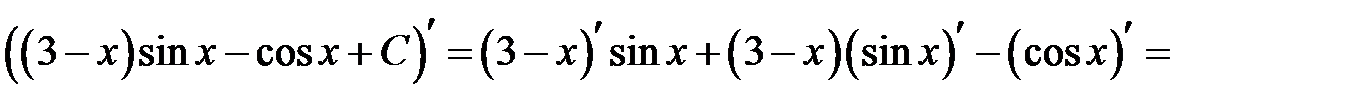
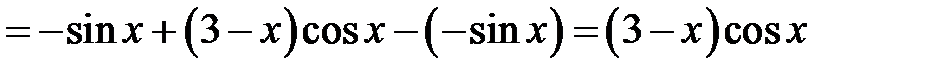
34. а)

 

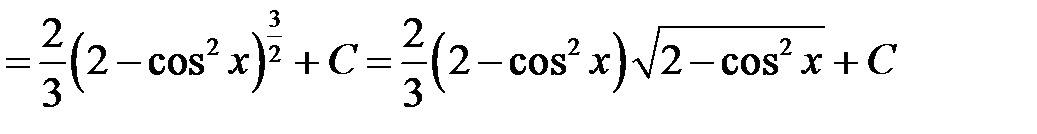
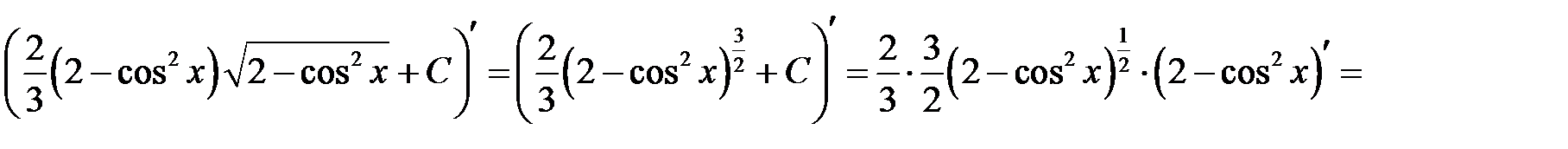
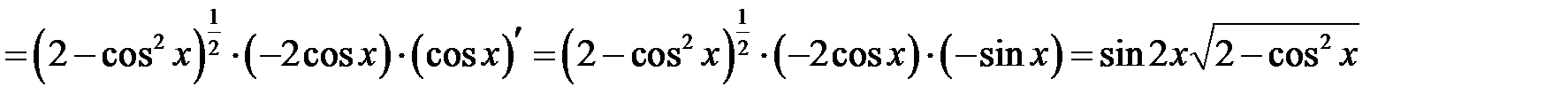
б)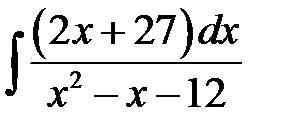

 

 

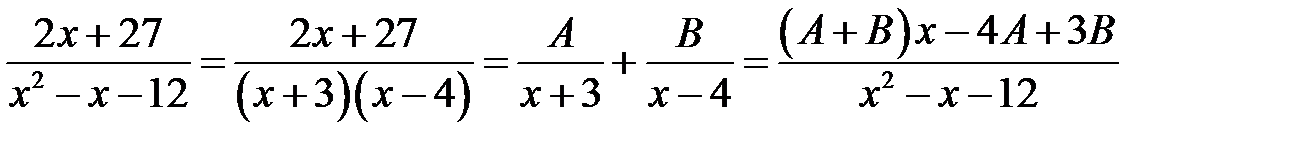
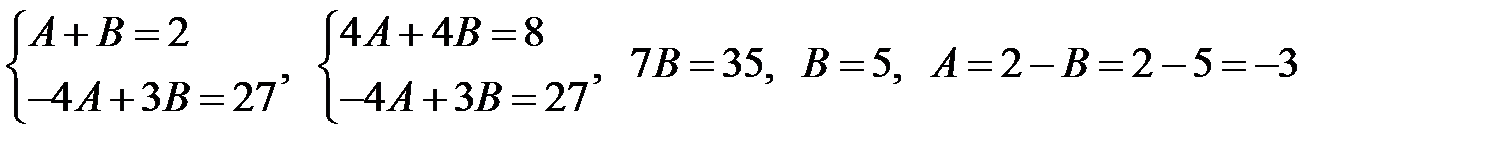
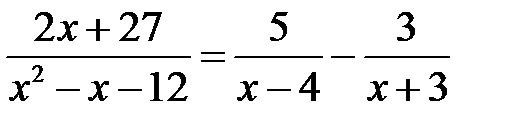
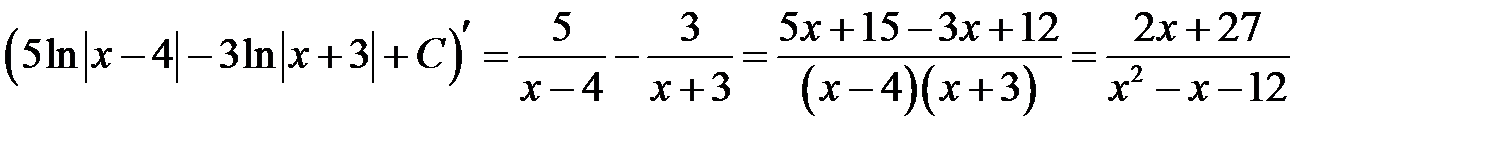
в)

 

 

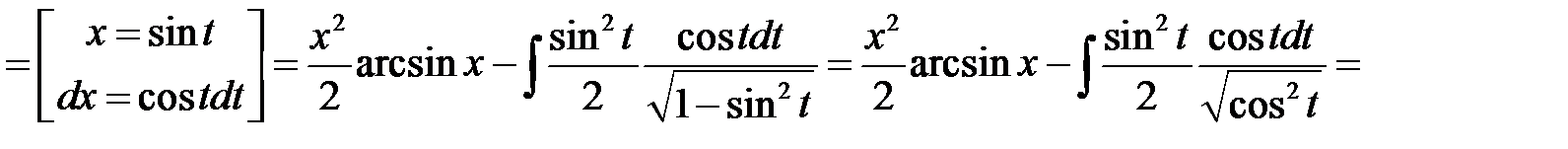
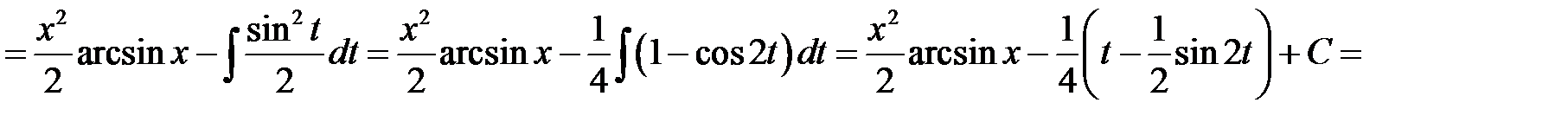
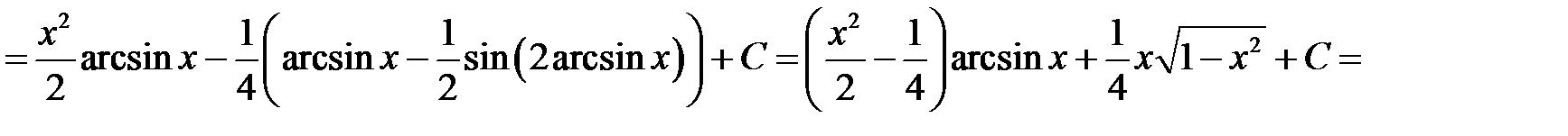
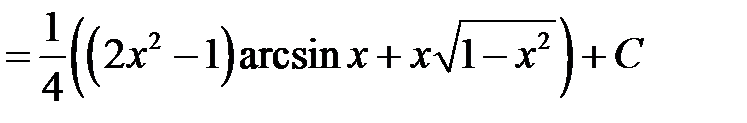
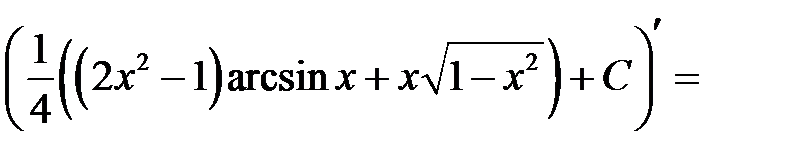
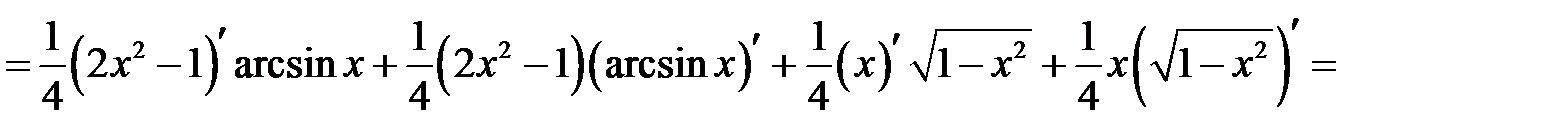
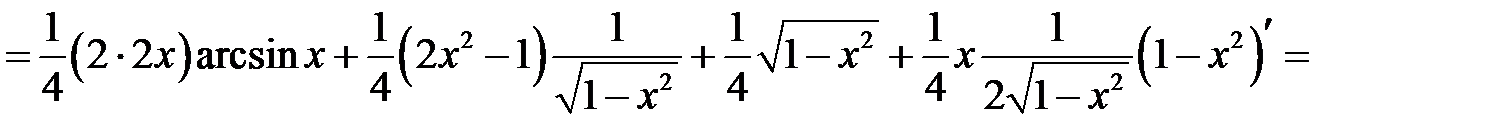
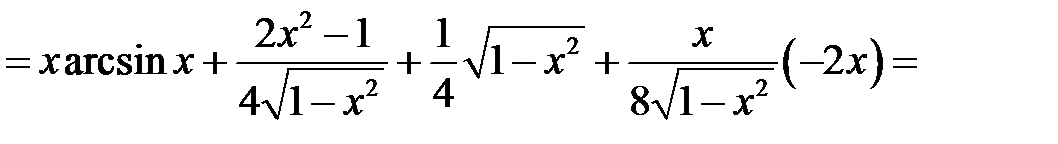
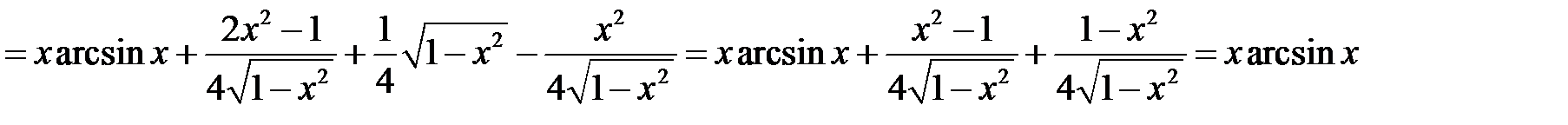
Вычислить площадь фигуры, ограниченной линиями

 

 

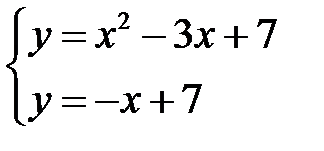
Построим заданную фигуру:

 

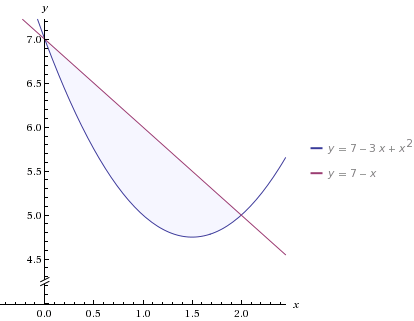
Получаем область интегрирования:

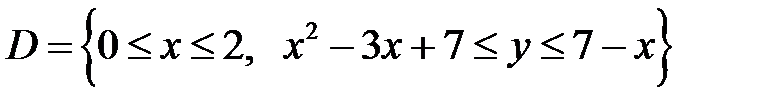
Получаем:

 

 

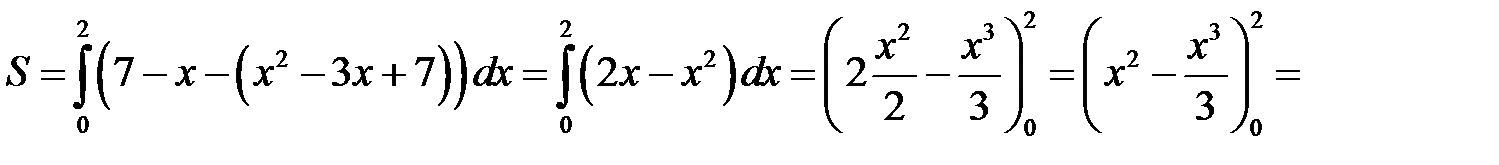
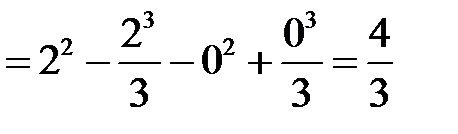
54.

 

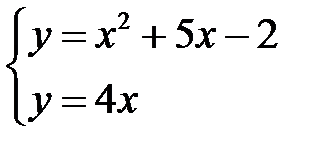
Построим заданную фигуру:

 

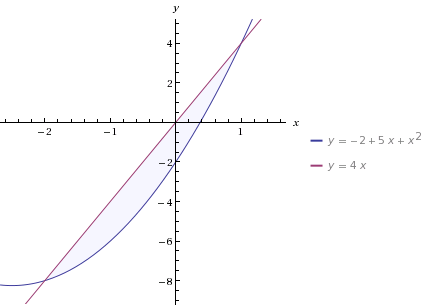
Получаем область интегрирования:

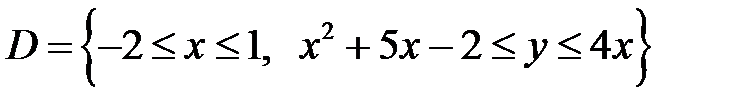
Получаем: