Объемы и поверхности тел

Формулы сокращенного умножения

(а+b)² = a² + 2ab + b²

(а-b)² = a² - 2ab + b²

a² – b² = (a-b)(a+b)

a³ – b³ = (a-b)( a² + ab + b²)

a³ + b³ = (a+b)( a² - ab + b²)

(a + b)³ = a³ + 3a²b+ 3ab²+ b³

(a - b)³ = a³ - 3a²b+ 3ab²- b³

Свойства степеней

a⁰ = 1 (a≠0)

a^m/n = 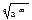(a≥0, n ε N, m ε N)

a^{- r} = 1/ a ^r (a>0, r ε Q)

a ^m · a ⁿ = a ^{m + n}

a ^m : a ⁿ = a ^{m – n} (a≠0)

(a ^m) ⁿ = a ^mn

(ab) ⁿ = a ⁿ b ⁿ

(a/b) ⁿ = a ⁿ/ b ⁿ

 

 

Первообразная

Если F’(x) = f(x), то F(x) - первообразная

для f(x)

Функция f(x) = Первообразная F(x)

k = kx + C

xⁿ = xⁿ⁺¹/n+1 + C

1/x = ln |x| + C

e^x = e^x + C

a^x = a^x/ ln a + C

1/√x = 2√x + C

cos x = sin x + C

1/ sin² x = - ctg x + C

1/ cos² x = tg x + C

sin x = - cos x + C

1/ x² = - 1/x

 

 

Геометрическая прогрессия

b _n+1 = b_n · q, где n ε N

q – знаменатель прогрессии

b _n = b₁ · q ^{n – 1} – n-ый член прогрессии

Сумма n-ых членов

S _n = (b _n q - b ₁ )/q-1

S _n = b ₁ (q ⁿ - 1 )/q-1

Модуль

|a| = a, если a≥0

-a, если a<0

Формулы cos и sin

sin (-x) = -sin x

cos (-x) = cos x

sin (x + π) = -sin x

cos (x + π) = -cos x

sin (x + 2πk) = sin x

cos (x + 2πk) = cos x

sin (x + π/2) = cos x

 

 

Объемы и поверхности тел

1. Призма, прямая или наклонная,параллелепипед V = S·h

2. Прямая призма S_БОК = p·h, p – периметр или длина окружности

3. Параллелепипед прямоугольный

V = a·b·c; P = 2(a·b + b·c + c·a)

P – полная поверхность

4. Куб: V = a³ ; P = 6 a²

5. Пирамида, правильная и неправ.

S = 1/3 S·h; S – площадь основания

6. Пирамида правильная S =1/2 p·A

A – апофема правильной пирамиды

7. Цилиндр круговой V = S·h = πr²h

8. Цилиндр круговой: S_БОК = 2 πrh

9. Конус круговой: V=1/3 Sh = 1/3 πr²h

10. Конус круговой: S_БОК = 1/2 pL= πrL

 

Тригонометрические уравнения

sin x = 0, x = πn

sin x = 1, x = π/2 + 2 πn

sin x = -1, x = - π/2 + 2 πn

cos x = 0, x = π/2 + 2 πn

cos x = 1, x = 2πn

cos x = -1, x = π + 2 πn