Аппроксимация и устойчивость разностной схемы

Разностная схема (4) аппроксимирует исходную дифференциальную задачу (1) - (2) на ее решении 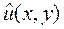если

при .

Разность называется невязкой.

Покажем, что невязка при .

Так как

 

 

то, заменяя здесь и соответствующими разложениями решения по формуле Тейлора в точке :

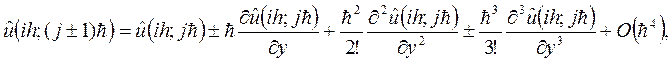получаем

 

Следовательно, и разностная схема (4) обладает свойством аппроксимации.

Разностная схема (4) называется устойчивой, если для достаточно малых шагов сетки и выполнены условия:

1) Для любой сеточной функции уравнение имеет единственное решение (существует обратный оператор ).

2) Существует константа , независящая от ( и ), такая, что для решения уравнения имеет место неравенство

(норма обратного оператора равномерно по ограничена константой : ).

Замечание.Условие 2) определения устойчивости разностной схемы принято называть условием устойчивости.

 

Проверку устойчивости разностной схемы (4) разобьем на несколько этапов.

Предложение 1.Пусть сеточная функция определена на всей сетке и отлична от константы (не все координаты вектора равны одному и тому же числу). Пусть на множестве внутренних узлов сетки имеет место неравенство

Тогда сеточная функция принимает свое наибольшее значение в одном из граничных узлов сетки

Предложение 2.Пусть сеточная функция определена на всей сетке и отлична от константы. Пусть на множестве внутренних узлов сетки имеет место неравенство

Тогда сеточная функция принимает свое наименьшее значение в одном из граничных узлов сетки

Из Предложений 1 и 2 немедленно следует

Предложение 3.Если существуетсеточная функция определенная на всей сетке , такая, что на множестве внутренних узлов сетки имеет место равенство

то она достигает своего наибольшего и наименьшего значений на множестве граничных узлов

Отсюда немедленно получаем выполнение условия 1) определения устойчивости разностной схемы. Действительно из предложения 3 следует, что однородная разностная схема для всех имеет только нулевое решение для всех Таким образом, неоднородное уравнение имеет единственное решение для любой сеточной функции

Перейдем к доказательству условия устойчивости.

Заметим, что для любого многочлена второй степени

имеет место равенство

 

 

Положим

где

Введем оператор :

Имеем

Рассмотрим разность где - решение разностной схемы.

Очевидно, что

Так как для то из Предложения 1 следует, что сеточная функция достигает своего наибольшего значения в одном из граничных узлов и, следовательно, или во всех узлах сетки .

Теперь рассмотрим сеточную функцию . Применив к этой функции оператор , получим

 

Так как для то из Предложения 2 следует, что сеточная функция достигает своего наименьшего значения в одном из граничных узлов и, следовательно, или во всех узлах сетки .

Таким образом,

во всех узлах сетки . Следовательно,

и условие устойчивости для разностной схемы (4) выполняется с константой .

По теореме Филиппова из аппроксимации и устойчивости разностной схемы получаем ее сходимость:

при ,

здесь - решение разностной схемы (3) (или что тоже самое (4)), - точное решение исходной дифференциальной задачи (1) – (2).