МОЩНОСТЬ И КПД КОМПРЕССОРА

Мощность и КПД компрессора.Мощность компрессора:

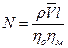, (12.21)

где ρ – плотность газа, поступающего в компрессор, кг / м³; 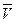- объёмная подача компрессора, м³ / с; l – удельная работа компрессорного процесса, Дж / кг; η_о- объёмный коэффициент, учитывающий потери объёма газа вследствие перетекания через зазоры уплотнений компрессора; η_м- механический КПД компрессора, учитывающий расход энергии на преодоление механического трения и привод вспомогательных механизмов (масляных насосов, вентиляторов и насосов системы охлаждения, если они приводятся от вала компрессора).

Числовые значения η_ои η_м для компрессоров различных типов приведены в соответствующих разделах учебного пособия.

Что касается КПД, то вместо истинного его значения используется значение, получаемое при замене реального рабочего процесса схематизированным. Принимают, что процесс сжатия происходит по политропе с постоянным показателем n:

,

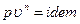считая, что газовый поток однородный.

Удельная работа изменения давления при таком процессе

.

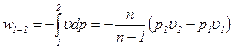Используя понятие «характеристика сжатия»

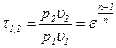, (12.22)

получим следующие варианты предыдущей формулы:

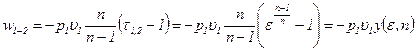. (12.23)

Вспомогательную функцию двух аргументов

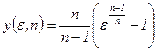, (12.24)

можно определить по графику (рис. 12.7).

 

 

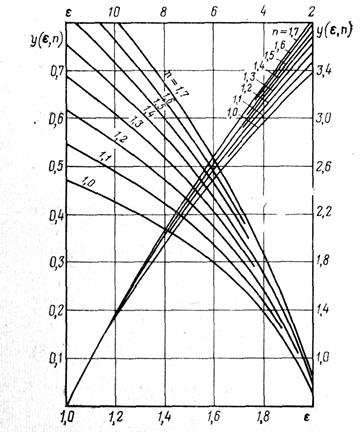
Рис. 12.7. График вспомогательной функции y (ε, n)

 

Показатель политропы n выбирают применительно к реальному процессу.

Если процесс близок к адиабатическому, принимают n = k, где k – показатель адиабаты (для идеального газа), определяемый по составу газа.

Из формулы (12.23) и формулы для определения l вытекают выражения адиабатической удельной работы, адиабатической мощности и внутреннего адиабатического КПД:

; ; .

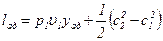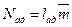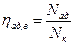Здесь N_к - внутренняя мощность компрессора. Как и для насоса, это – мощность взаимодействия рабочих органов с потоком текучей среды, в данном случае – газа.

Заметим, что для учёта влияния на КПД внешних утечек с массовым расходом 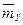адиабатическая мощность подсчитывается по «полезной» части массового расхода на входе в компрессор:

.

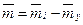Если пренебречь изменением кинетической энергии газа, то формулу адиабатической мощности можно представить так:

,

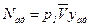где .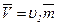

Аналогичные выражения получают для изотермического процесса сжатия, который служит эталоном для такого реального процесса, в котором текущая температура газа мало отличается от начальной.

При n = 1 (изотерма идеального газа) выражение (12.24) приводит к неопределённости. Используя условие 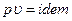для вычисления интеграла w_1-2, видим, что y_из = ln ε. Изотермическая мощность и внутренний изотермический КПД:

; .

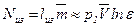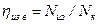Подобным же образом для других числовых значений n формулируются понятия политропической мощности и внутреннего политропического КПД:

; .

Приведенные формулы можно использовать:

1) при испытании действующего компрессора с целью построения графика его характеристики;

2) для определения потребной мощности проектируемой компрессорной установки.

В первом случае измеряют расход газа и мощность компрессора, а затем вычисляют тот или другой КПД. Об определении значения n для внутреннего политропического КПД говорится далее. Относительный КПД¹ в данном случае является, как и внутренний КПД насоса, показателем режима, а при сравнении однотипных машин – также критерием эффективности затраты энергии на сжатие газа в одинаковых условиях.

 

____________

¹ Собирательный термин для величин η_ад.в, η_из.в, η_пол.в.

Чем ближе реальный процесс к выбранному эталонному, тем меньше относительный КПД отличается от внутреннего КПД.

Во втором случае внутреннюю мощность можно вычислить так:

Вариант формулы выбирают в зависимости от того, какой КПД известен по статистическим данным испытаний компрессоров данного типа. Здесь относительный КПД выполняет другую роль: он служит коэффициентом мощности, т. е. поправкой, позволяющей перейти от теоретической мощности N_ад (или N_из, или N_пол), рассчитываемой по условиям перекачивания газа, к реальной внутренней мощности компрессора.

М о щ н о с т ь к о м п р е с с о р а – сумма внутренней мощности и мощности механического трения (потери мощности в частях машины, изолированных от потока газа): N = N_к + N_м.

М е х а н и ч е с к и й КПД .

И з о т е р м и ч е с к и й КПД .

Аналогичные определения – для адиабатического и политропического КПД.

М о щ н о с т ь н а в а л у к о м п р е с с о р а , где N_всп - мощность вспомогательных механизмов (масляного насоса, вентилятора и др.).

Совершенство компрессорного процесса оценивают при помощи относительных термодинамических КПД – изотермического η_из и изоэнтропного η_а.

Если действительный политропный процесс протекает в компрессоре с показателем n при удельной энергии l, то изотермический и изоэнтропный КПД

; (12.25)

. (12.26)

Здесь l_из и l_а - удельные работы изотермического и изоэнтропного процессов, определяемые формулами (12.13) и (12.15).

Изотермический КПД η_из применяют для оценки компрессоров с интенсивно действующим водяным охлаждением (поршневых и роторных). Для этих компрессоров изотермический процесс, обладающий наименьшей удельной энергией, является эталонным.

Компрессоры с неинтенсивным охлаждением (центробежные и осевые) оцениваются при помощи изоэнтропного КПД η_а. Это объясняется тем, что для компрессоров этого типа изоэнтропный процесс является эталонным, наиболее совершенным.

Значения η_из и η_а для компрессоров различных типов приведены далее.

Установим основные, важные в расчётной практике соотношения, связывающие относительный изоэнтропный КПД с термодинамическими параметрами торможения процесса.

Из формул (12.1) и (12.10) следует

.

Действительный процесс является политропным, и для него формулу (12.17) можно записать в параметрах торможения при условии q = 0 так:

. (12.27)

Из этих соотношений следует

. (12.28)

Формула для расчёта относительного изотермического КПД для оценки объёмных одноступенчатых компрессоров с интенсивным охлаждением получается из (12.15) и (12.25):

. (12.29)

Расчёт с использованием параметров торможения здесь не имеет смысла, потому что в начале и конце процесса сжатия скорости газового потока незначительны.