ТЕРМОДИНАМИКА КОМПРЕССОРНОГО ПРОЦЕССА

Простейшая теория компрессорных машин, обладающая практически приемлемой точностью, основывается на термодинамике идеального газа, подчиненного уравнению

. (12.1)

При конечном давлении воздушного компрессорного процесса более 10 МПа следует пользоваться уравнением состояния реального газа

, (12.2)

где z – коэффициент сжимаемости. Опытные значения его в зависимости от безразмерных величин p / p_кр и T / T_кр приведены в технической справочной литературе (например, Шерстюк А. Н. Насосы, вентиляторы, компрессоры. М.: Высшая школа, 1972, 342 с.).

Основные уравнения.Совместное использование первого закона термодинамики и уравнения состояния идеального газа приводит к следующим уравнениям процессов сжатия и расширения, происходящих в компрессорах:

политропный процесс (12.3)

адиабатный процесс (12.4)

изотермический процесс 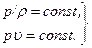(12.5)

Политропный процесс является общим видом термоди­намического процесса и протекает в компрессорах в зави­симости от внешних и внутренних условий с показателем n = 1,15 - 1,80.

Адиабатным называют процесс без теплообмена с внеш­ней средой; в таком процессе возможно внутреннее образо­вание теплоты за счет работы газового трения и вихреобразования. Строго адиабатный процесс в компрессорах получить нельзя вследствие невозможности полной тепло­вой изоляции газового потока от окружающей среды.

Кроме процессов (12.3) - (12.5) в теории компрессоров рассматривают процесс изоэнтропный, характеризующий­ся постоянством энтропии в результате отсутствия тепло­обмена с окружающей средой и внутреннего тепловыделе­ния, обусловленного газовым трением в потоке. В реаль­ных компрессорах, очевидно, изоэнтропный процесс невоз­можен.

Диаграммы ST и pv.Указанные процессы удобно изображать графически в координатах S, T (рис. 12.5.).

 

 

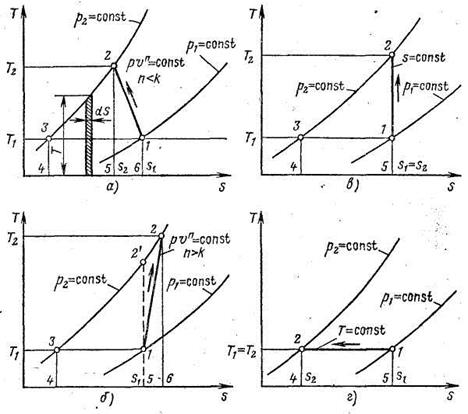
Рис. 12.5. S, T - диаграммы компрессорных процессов,

описываемых формулами (12.3) – (12.5).

 

Здесь представлены основные виды компрессорных процессов: политропный n < k, свойственный компрессорам с интенсивным водяным охлаждением (рис. 12.5, а);

политропный n > k, типичный для лопастных (центробежных и осевых) компрессоров (рис. 12.5, б);

изоэнтропный с S = const (рис.12.5, в);

изотермический с T = const (рис. 12.5, г).

Процессы на рис. 12.5, в и г в компрессорах неосущест­вимы, первый - потому что образование теплоты за счет внутреннего газового трения проявляется весьма существенно, второй - по причине невозможности выполнить конструкцию охлаждающей системы компрессора так, что­бы она обеспечивала сжатие газа при постоянной темпера­туре. Как будет показано ниже, эти два процесса исполь­зуются для оценки энергетической эффективности компрес­соров.

Отметим свойства термодинамических диаграмм комп­рессорных процессов, показанных на рис. 12.5.

Процесс сжатия во всех случаях представляется ли­ниями 1-2. В случаях на рис. 12.5, а и б сжатие (повыше­ние давления) сопровождается изменением энтропии и повышением температуры газа. При этом увеличивается эн­тальпия газа.

В политропном компрессорном процессе при n < k ли­ния 1-2 представляет собой процесс сжатия, протекающий в рабочей полости (цилиндре, каналах колеса и корпуса) компрессоров; линия 2-3 - процесс изобарного охлажде­ния сжатого газа, уходящего из компрессора. Этот процесс протекает в охладителе компрессора и трубопроводной сети.

Соответственно закону сохранения энергии работа, за­трачиваемая компрессором на сжатие и выталкивание газа (без учета механических потерь), представляется сум­мой теплот, отводимых от газа в процессах сжатия и изо­барного охлаждения.

Воспользуемся основным определением энтропии в эле­ментарном тепловом процессе:

.

Для процессов 1-2 и 2-3

; .

Подынтегральные произведения являются элементар­ными площадями процессов сжатия и охлаждения, изобра­женных в ST - диаграмме. Следовательно, количество энергии в тепловых единицах, подводимое к газу для осущест­вления компрессорного процесса, представляется суммой площадей диаграммы 1-2-5-6 и 2-3-4-5.

При сжатии газа по политропе с показателем n > k (рис. 12.5), что характерно для компрессоров с воздушным или неинтенсивным водяным охлаждением, площадь 1-2-6-5 под политропой 1-2 процесса сжатия представляет собой количество теплоты, образующейся в потоке вследст­вие газового трения и вихреобразования.

Энергия, подводимая к компрессору, расходуется на проведение компрессорного процесса (сжатие и проталки­вание) и работу газового трения в проточной полости. Ра­бота компрессорного процесса представляется площадью 1-2-3-4-5. Следовательно, полная энергия, расходуемая компрессором (без энергии, идущей на покрытие механи­ческих и объемных потерь), выражается площадью 2-3-4-6.

Если бы процесс в компрессоре протекал по изоэнтропе 1-2', то полная затрата энергии была бы равна площади 1-2'-3-4-5, т. е. была бы меньше на размер площади 1-2'-2-6-5. Следовательно, увеличение энергии, расходуе­мой компрессором, при переходе от изоэнтропного процес­са к реальному политропному с n > k сопровождается увеличением потребления энергии, равным площади 2'-2-6-5-1. Очевидно, площадь 1-2'-2 представляет собой энергию, за­трачиваемую дополнительно на сжатие и проталкивание объема, появляющегося в ре­зультате нагрева газа в про­цессе трения и вихреобразования.

Изложенные соображения применимы и к рассмотрению S, T - диаграмм изоэнтропного и изотермического процессов (рис. 12.5, в и г).

Наименьшее количество энергии затрачивается в ком­прессорном процессе с изотер­мическим сжатием (рис. 12.5, г). Эта энергия представ­ляется площадью 1-2-4-5.

 

Рис. 12.6. - диаграммы компрессорных процессов,

описываемых формулами (12.3) – (12.5)

 

В некоторых случаях удоб­но изображать компрессорные процессы на р, 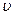- диаграмме (рис. 12.6). Здесь сплош­ной линией 1-2 показан процесс при политропном сжатии с n < k, протекающий в проточной полости компрессора. Процесс охлаждения 2-3 теоретически проходит по изобаре р₂ = const, в действительных условиях несколько отклоняет­ся от изобары.

Изотермическое сжатие изображается штриховой лини­ей 1-2", изоэнтропное - 1-2', адиабатное при n > k - лини­ей 1-2"'.

Уравнения работы компрессорных процессов. Поскольку компрессоры, как и насосы, служат для перемеще­ния текущих тел, к ним формально применимы понятия, используемые в качестве технических показателей насосов: удель­ная полезная работа или напор, полезная мощность, к. п. д.

Действительно, выражение работы, переданной потоку газа рабочими органами компрессора, полученное из баланса работ в проточной машине, выглядит так же, как для насосов:

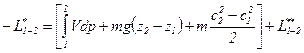
отличаясь тем, что работа изменения давления (-W_{1 -2}) опре­делена не по разности конечного и начального давлений V (р₂ – р₁), а интегралом.

Переходя к удельным величинам, отделяя потери и пренебрегая вследствие малости слагаемым g (z₂ - z₁), получим выражения удельной полезной работы и напора:

;

,

где 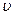- удельный объём ( 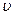= V / m); 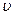= 1 / ρ.

Понятие «давление» в том смысле, которое оно имеет для насосов, для компрессоров не существует, так как V и ρ - переменные.

Поэтому определения l и H – формальные. Дело в том, что для вычисления интеграла главной части полезной работы (работы изменения давления ) необходимо проследить за всеми особенностями сложного процесса сжатия газа в компрессоре. Сложность в том, что, во-первых, зависимость V = f (p) в интеграле работы определяется условиями теплообмена (его направлением и интенсивностью), которые, в свою очередь, зависят от системы охлаждения машины, и, кроме того, изменяются с температурой сжимаемого газа на его пути от всасывающего до нагнетательного патрубка. Во-вторых, газовый поток неоднороден в том смысле, что состояние газа в различных частях потока изменяется по-разному. Некоторая часть потока газа (перетекания или остатки газа в компрессорной камере) имеет параметры, отличающиеся от параметров основной части потока. Определение средних параметров неоднородного потока сопряжено с большими трудностями.

Вследствие этого понятие полезной работы и производные его (т. е. l, H, p, N_п) как количественные показатели действия компрессора практического значения не имеют. Их функции (выражать нагрузку на машину и определять к. п. д.) выполняют другие величины.

На графике характеристики компрессора указывают непосредственно конечное p₂ и начальное давления p₁ (средние их значения) или с т е п е н ь п о в ы ш е н и я д а в л е н и я ε = p₂ / p₁.

Удельная работа l, затрачиваемая в компрессорном процессе при сжатии и выталкивании 1 кг массы газа, выражается площадью р, 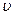- диаграммы, ограниченной изобарами начального р₁ и ко­нечного p₂ давлений, политропой сжатия и осью ординат (рис. 12.б).

Для процесса с n < k

.

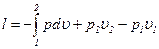Из уравнения политропного сжатия имеем и, следовательно,

.

После интегрирования и алгебраических преобразований получается

. (12.6)

Связь между давлениями и температурами в политропных процессах определяется соотношением

. (12.7)

Поэтому

. (12.8)

Присоединив к формуле (12.8) уравнение состояния, записанное для начальных параметров, , получим

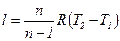. (12.9)

Уравнения политропного и изоэнтропного процессов (12.3) и (12.4) совершенно идентичны и разнятся только значением показателей. Поэтому для изоэнтропного компрессорного процесса можно записать следующие соотношения:

; (12.10)

; (12.11)

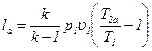; (12.12)

. (12.13)

Последние с помощью известных соотношений и легко преобразуется в уравнение

, (12.14)

выражающее работу изоэнтропного компрессорного процесса через начальную и конечную энтальпии сжимаемого газа.

Для изотермического компрессорного процесса из - диаграммы имеем

.

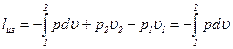Имея в виду, что 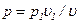, получаем

,

или

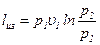. (12.15)

Приведенные соотношения (12.6) - (12.15) позволяют определять затраты энергии на проведение компрессорного процесса, но не дают открытого ответа на вопрос о распределении израсходованной энергии на изменение отдельных параметров процесса.

Последнее может быть выполнено использованием ус­ловия сохранения энергии: энергия, расходуемая в комп­рессорном процессе, идет на изменение энтальпии и кинетической энергии газа и покрытие потерь в окружающую среду. Это условие можно записать в самом общем виде как уравнение баланса энергии компрессорного процесса

, (12.16)

или

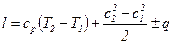. (12.17)

В теории и расчетах компрессорных процессов принято использовать параметры торможения. Напомним сущность этого понятия.

Если изоэнтропный газовый поток с температурой Т и скоростью c полностью затормаживается, то его кинетическая энергия превращается в теплоту и температура газа повышается до Т*, называемой температурой торможения. Очевидно, соотношение баланса энергии

;

. (12.18)

Следовательно, в соответствии с (12.17) удельная энергия изоэнтропного процесса может быть выражена через температуры торможения:

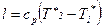. (12.19)

Давления и температуры в изоэнтропных процессах связаны соотношением (12.11). Поэтому параметр давления торможения может быть определён из этого уравнения:

. (12.20)

Подача компрессора.Расход газа на входе в компрессор и выходе из него различен не только по объёму, что обусловлено сжатием перекачиваемого газа, но и по массе. Последнее объясняется:

а) негерметичностью машины (внешние утечки и подсасывание воздуха из атмосферы через уплотнения вала и (или) штока);

б) выпадением из поступающего газа различных жидкостей (воды, смазочного масла, газового конденсата);

в) неполным отделением впрыскиваемой (для охлаждения, уплотнения зазоров смазки) жидкости.

Поэтому различают следующие величины:

1. О б ъ ё м н ы й р а с х о д г а з а н а в х о д е в к о м п р е с с о р 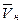. Соответствующий массовый расход , где ρ_н - начальная плотность газа.

2. М а с с о в а я п о д а ч а к о м п р е с с о р а 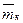- массовый расход газа в контрольном сечении на выходе из компрессора. При измерении объёмного расхода газа в том же сечении массовая подача определяется по формуле , где ρ_к - конечная плотность газа.

3. О б ъ ё м н а я п о д а ч а с у х о г о г а з а 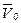- объёмный расход на выходе, пересчитанный на условия состояния газа, соответствующие стандарту.¹

 

________________

¹ По ГОСТ 2939 – 63: 20°C, 760 мм рт. ст., относительная влажность = 0.

Черта над символами здесь и ниже означает расход (в отличие от объёма или массы – без ……черты).

Объёмный расход 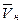зависит от размеров компрессора, частоты циклов действия и режима работы, в меньшей степени - от состава и температуры всасываемого газа. В отличие от 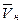, массовый расход зависит также от плотности поступающего газа, вследствие чего значение 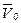привязано к определённым начальным условиям (см. примечание ¹ на предыдущей странице).