Линейные операции над n-мерными векторами.

Векторная алгебра

 

N – мерные векторы.

 

1. Линейные операции над n – мерными векторами.

2. Разложение вектора по системе векторов.

 

Введение. Пространство можно определить, как некоторое множество, имеющее структуру.

Пространство считается заданным, если между объектами множества установлены вполне определенные отношения и (или) определены некоторые операции.

Поскольку понятие пространства сформировалось в результате абстрагирования и обобщения трёхмерного евклидового пространства, то в пространстве обычно фиксируются отношения сходные по формальным признакам с этим пространством.

Наиболее характерным среди них является расстояние.

Исторически первым сформировалось понятие 3-х мерного геометрического пространства, которое в дальнейшем обобщалось и трансформировалось.

Один из вариантов обобщения:

- увеличение размерности объектов, составляющих пространство вплоть до объектов бесконечной размерности.

- переход от числовых последовательностей как элементов пространства к объектам, имеющим самую различную природу.

Возможность перехода от трехмерных векторов к многомерным появилась тогда, когда вектор стали рассматривать, как упорядоченную последовательность n чисел.

 

Пример 1 (многомерного пространства)

Каждая точка фазового пространства характеризуется упорядоченным набором параметров, описывающих состояние объекта рассмотрения.

Экономическое состояние предприятия может характеризоваться:

Стоимостью основных фондов, количеством работников, объемом выпускаемой продукции, её себестоимостью и т.п., которые в совокупности можно рассматривать в n – мерном пространстве, а изменения экономического состояния – как траекторию (годограф) движения в этом пространстве состояний.

 

Пример 2 Трехмерное цветовое пространство, состоящее из векторов, компоненты которого суть интенсивности красного, зелёного и синего цветов.

Изменяя, интенсивность этих 3-х цветов и накладывая, их потом друг на друга, можно получать цветовую палитру с неограниченным числом различных оттенков. На этом принципе основана работа цветных электроннолучевых трубок в телевизорах и мониторах компьютеров.

Формально переход от одного цвета или оттенка к другому можно описать перемещением от точки к точке в 3-х мерном цветовом пространстве. При этом изменение цвета можно измерять количественно, используя операции над векторами.

 

Линейные операции над n-мерными векторами.

 

Пусть на каком-нибудь множестве объектов определены действия сложения и умножения на число. Это означает, что указанные действия имеют смысл и результатами их действий являются элементы того же самого множества.

Например: сложение определено на множестве матриц одной размерности, а для матриц различной размерности сложение не имеет смысла.

- умножение на вещественное число во множестве целых чисел неопределенно, т.к результатом такого умножения может оказаться нецелое число (объект другого множества)

 

Определение. Линейным пространством называется множество, на котором определены операции сложения и умножения на число, удовлетворяющее следующим условиям:

1. Коммутативность:

2. Ассоциативность: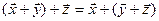

3. Существует нулевой элемент 0 такой, что для любого x

4. Для любого элемента 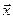существует противоположный ему элемент 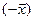такой, что

5. Пусть c и d - числа, тогда:

6.

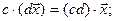
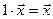
7.

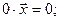
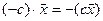
Примерами линейного пространства является:

- пространство действительных чисел.

- множество геометрических векторов на плоскости.

- пространство матриц фиксированной размерности.

- пространство решений однородных линейных систем и др.

Будем рассматривать в качестве элементов линейного пространства

n- мерные векторы, как упорядоченные наборы из n вещественных чисел, называемых координатами или компонентами векторов, т.е .

Линейное пространство таких n-мерных векторов называют

n-мерным вещественным векторным пространством и обозначают Rⁿ числа x_i(i=1,…n)-составляющие вектора,

n- размерность вектора.

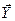Определение. Сумма n- мерных векторов и новый n - мерный вектор 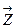, составляющие которого равны суммам соответствующих составляющих складываемых векторов, т.е.

Складывать можно лишь векторы одинаковой размерности

(3:-1;9)+(6;2) – не определена. (6;2) 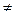(6;2:0)

Пусть дано m векторов 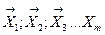, тогда линейная комбинация этих векторов выглядит так:

Скалярное произведениевекторов и 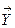называется число равное сумме парных произведений соответствующих составляющих этих векторов, т.е

 

Определение. Вещественное векторное пространство в котором введено скалярное произведение, называется Евклидовым пространством