Пример 2.

Крестьянские хозяйства подразделяются по размерам земельных угодий следующим образом:

Земельные угодья, га	Число хозяйств, ед.
До 3
4 – 5
6 – 10
11 – 20
21 – 50
51 – 70
71 – 100
101 – 200
201 и больше

 

Рассчитать:

1) средний размер земельных угодий;

2) показатели вариации: размах, среднее линейное отклонение, среднее квадратическое отклонения, коэффициент вариации; оценить количественную однородность совокупности;

3) моду и медиану.

 

Решение

 

Для расчета требуемых показателей следует перейти от вариационного ряда к дискретному. Для этого находится середина каждого интервала. Расчет показателей выполним в табличном виде:

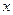
Земель-ные угодья, га	Число хо-зяйств, ед.							Нако- плен-ные час-тоты	Плот-ность
До 3		2,5		57,4		3294,76	98842,8
4 – 5		4,5		55,4		3069,16	153458,0
6 – 10				51,9		2693,61	1077444,0
11 – 20		15,5		44,4		1971,36	1577088,0
21 – 50		35,5		24,4		595,36	1071648,0
51 – 70		60,5		0,6		0,36	216,0
71 – 100		85,5		25,6		655,36	458752,0		23,3
101 – 200		150,5		90,6		8208,36	5745852,0
201 и больше		250,5		190,6		36328,36	4359403,2		1,2
Итого			∑=311360		∑=209264		∑=14542704

 

1. Средний размер земельных угодий на одно крестьянское хозяйство определяется по формуле:

,

где среднее значение признак; серединное значение интервала, в котором изменяется варианта (значение) усредняемого признака; частота, с которой встречается данное значение усредняемого признака.

(га).

2. К показателям вариации относятся:

а) размах вариации:

,

где максимальное значение признака (максимальное серединное значение интервала), минимальное значение признака;

б) среднее линейное отклонение:

;

в) среднее квадратическое отклонение:

;

г) коэффициент вариации:

.

Рассчитаем указанные показатели вариации.

Размах вариации:

(га).

Среднее линейное отклонение:

(га).

Среднее квадратическое отклонение:

(га).

Коэффициент вариации:

(88,2 %).

Крестьянские угодья количественно неоднородны по размеру земельных угодий.

3. Мода и медиана относятся к особому виду средних величин – структурным средним.

Мода – это наиболее часто встречаемое значение признака.

Медиана – величина признака у единицы, находящейся в середине упорядоченного ряда.

В интервальных рядах распределения структурные средние рассчитываются по особым формулам.

При расчете моды можно применить следующую формулу:

.

Здесь начало модального интервала, модальный интервал – интервал, в котором достигает максимума величина отношение частоты интервала к его величине; величина соответственно модального, до- и послемодального интервалов; частота до- и послемодального интервалов соответственно.

Примечание

В случае равных интервалов формула моды примет привычный вид:

.

Медиана рассчитывается по формуле:

,

где нижняя граница медианного интервала; величина медианного интервала; половина от общего числа наблюдений; сумма накопленных частот до начала медианного интервала; частота медианного интервала.

Рассчитаем структурные средние:

А. Определяем модальный интервал, в данном примере их два: [6 – 10] и [11 – 20]. Для расчета моды подставим в формулу все переменные:

(га).

 

(га).

Следовательно, наиболее часто встречаемый размер земельных угодий – 11 га.

Б. Для расчета медианы определяем медианный интервал – это тот интервал, в котором находится крестьянское хозяйство. В данном примере – интервал [21 – 50].

Подставляем в формулу значения:

(га).

Следовательно, 50 % крестьянских хозяйств имеют размер земельных угодий меньше 42,6 га, а остальные 50 % – больше.

 

Тема 3. Выборочное наблюдение