ГЛАВА 1. ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
1.1. Предмет, метод, задачи и организация
Статистика– это наука, изучающая количественную сторону массовых явлений в неразрывной связи с их качественной стороной, количественное выражение закономерностей общественного развития.
Статистика как наука имеет пять особенностей.
Первая особенность статистики заключается в исследовании не отдельных фактов, а массовых социально-экономических явлений и процессов, выступающих как множества отдельных фактов, обладающих как индивидуальными признаками, так и общими признаками. Задача статистического исследования состоит в получении обобщающих показателей и выявлении закономерностей общественной жизни в конкретных условиях места и времени, которые проявляются лишь в большой массе явлений через преодоление случайности, свойственной единичным элементам.
Вторая особенность статистики состоит в том, что она изучает в первую очередь количественную сторону общественных явлений и процессов, но в отличие от математики, в конкретных условиях места и времени, т.е. предметом статистики являются размеры и количественные соотношения социально-экономических явлений, закономерности их связи и развития. При этом качественную определенность единичных явлений обычно определяют сопряженные науки.
Третья особенность статистики заключается в том, что она характеризует структуру, т.е. внутреннее строение массовых явлений (статистического множества) с помощью статистических показателей.
Четвертая особенность статистики заключается в исследовании изменений общественных явлений в пространстве и во времени. Изменения в пространстве (т.е. в статике) выявляются анализом структуры общественного явления, а изменения во времени (т.е. в динамике) - исследованием уровня и структуры явления.
Пятой особенностьюстатистики является выявление причинно-следственных связей отдельных явлений общественной жизни.
Под статистической методологиейпонимаетсясистема приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в структуре, динамике и взаимосвязяхсоциально-экономических явлений.
1.2. Статистическое наблюдение
Полный цикл статистического исследования включает следующие этапы:
1) сбор первичной информации (метод статистического наблюдения);
2) предварительную обработку данных (метод группировки, графический метод);
3) расчет и интерпретацию индивидуальных и сводных показателей (уровня, структуры и вариации, взаимосвязи и динамики);
4) моделирования и прогнозирования взаимосвязи и динамики исследуемых процессов и явлений.
Статистическое наблюдение – это планомерный систематический, базирующийся на научной основе сбор данных о явлениях и процессах общественной жизни посредством регистрации их наиболее важных признаков в соответствии с программой наблюдения.
План статистического наблюдения включает программно-методологическую и организационную части. В программно-методологической части указываются: цель, задачи и программа наблюдения, объект и единица наблюдения, совокупность признаков единицы наблюдения и инструментарий наблюдения (инструкцию по проведению наблюдения и статистический формуляр, содержащий программу и результаты наблюдения). В организационной части указываются: место и время наблюдения; перечень учреждений и организаций, ответственных за организацию и выполнение наблюдений, подготовку и расстановку кадров; выбор способов и регистрации сведений, перечень подготовительных мероприятий и т.д.
Статистические наблюдения классифицируют по форме, виду и способу наблюдения.
Наиболее распространенными формами статистического наблюдения являются: отчетность (предприятий, организаций, учреждений и т.п.) и специально организованные наблюдения с целью получения сведений, отсутствующих в отчетности (переписи, обследования, единовременные учеты).
Виды наблюдения различают: по времени наблюдения (непрерывные, периодические и единовременные) и по полноте охвата единиц статистической совокупности (сплошные и несплошные).
По способам статистического наблюдения различают: непосредственное, документальное наблюдения и опрос. В статистике применяются следующие виды опросов: устный (экспедиционный), саморегистрация (когда формуляры заполняются самими респондентами), корреспондентский, анкетный и явочный, с помощью современных средств вычислительной техники.
Показатели, используемые в экономико-статистическом анализе, характеризуют определенные категории и понятия, и расчет таких показателей должен проводиться путем теоретического анализа изучаемого явления. Поэтому в каждой конкретной области приложения статистики разрабатывается своя система статистических показателей.
1.3. Методы сплошного и выборочного наблюдения социально-экономических явлений и процессов
Задачей сплошного наблюденияявляется получение информации обо всех единицах исследуемой совокупности. Поэтому при проведении сплошного наблюдения важной задачей является формирование перечня признаков, подлежащих обследованию. От этого в конечном итоге зависит качество и достоверность результатов обследования.
До последнего времени российская статистика опиралась в первую очередь на сплошное наблюдение. Однако такой вид наблюдения имеет серьезные недостатки: высокую стоимость получения и обработки всего объема информации; большие затраты трудовых ресурсов; недостаточную оперативность информации, так как для ее сбора и обработки необходимо много времени. И, наконец, ни одно сплошное наблюдение, как правило, не обеспечивает полного охвата всех без исключения единиц совокупности. Большее или меньшее число единиц обязательно остается вне наблюдения как при проведении единовременных обследований, так и при получении сведений по такой форме наблюдения, как отчетность.
Например, при проведении сплошного статистического обследования малых предприятий по итогам работы за 2000 г. бланки форм (вопросники) были получены от 61% предприятий, которым были направлены вопросники. Причины неполучения ответов сведены в табл. 1.
Таблица 1
| Причина неполучения ответов | Доля предприятий, не приславших ответа |
| Адрес предприятия неправильно указан в едином государственном реестре | 15 % |
| Не осуществляли деятельность в 2000 г. | 14 % |
| Ликвидация предприятия на момент проведения обследования | 4 % |
| Отсутствие ответа по другим причинам | 6 % |
Количество и доля неохваченных единиц зависят от многих факторов: вида обследования (по почте, путем устного опроса); типа отчетной единицы; квалификации регистратора; содержания вопросов, предусмотренных программой наблюдения; времени дня или года проведения обследования и др.
Несплошное обследование изначально предполагает, что обследованию подлежит лишь часть единиц изучаемой совокупности. При его проведении следует заранее определить, какая часть совокупности должна быть подвергнута наблюдению и каким образом следует отобрать те единицы, которые должны быть обследованы.
Одним из преимуществ несплошных наблюдений является возможность получения информации в более короткие сроки и с меньшими затратами ресурсов, чем при сплошном наблюдении. Это связано с меньшим объемом собираемой информации, а следовательно, с более низкими затратами на ее получение, проверку достоверности, обработку и анализ.
Существует насколько видов несплошного наблюдения. Одно из них – выборочное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой совокупности, отобранных с помощью специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.
Преимущество выборочного наблюдения обеспечивается за счет:
1) экономии финансовых средств, затрачиваемых на сбор и обработку данных,
2) экономии материально-технических ресурсов (канцелярских товаров, оргтехники, расходных материалов, транспортного обслуживания и т. п.),
3) экономии трудовых ресурсов, привлекаемых на всех этапах выборочного наблюдения,
4) сокращения времени, затрачиваемого как на получение первичной информации, так и на ее последующую обработку вплоть до публикации итоговых материалов.
Главной проблемой при проведении выборочного исследования является то, насколько уверенно можно по свойствам отобранных объектов судить о действительных свойствах генеральной совокупности. Поэтому всякое такое суждение неизбежно имеет вероятностный характер, и задача сводится к обеспечению возможно большей вероятности правильного суждения.
Совокупность, из которой производится отбор, называется генеральной. Отобранные данные представляют собой выборочную совокупность или выборку. Для того, чтобы выборка полно и адекватно представляла свойства генеральной совокупности, она должна быть представительной или репрезентативной. Репрезентативность выборки обеспечивается только при объективности отбора данных.
Различают два вида выборочного наблюдения: повторный и бесповторный отбор.
При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после отбора отобранная единица возвращается в совокупность и снова может быть выбранной – «схема возвратного шара».
При бесповторном отборе отобранная единица не возвращается обратно, вероятность попадания остающихся единиц в выборку все время меняется – «схема безвозвратного шара».
Выделяют следующие способы отбора единиц из генеральной совокупности:
а) индивидуальный отбор, когда в выборку отбираются отдельные единицы,
б) групповой отбор, когда в выборку попадают качественно однородные группы или серии изучаемых единиц,
в) комбинированный отбор, представляющий собой комбинацию первых двух способов.
Возможны следующие методыотбора единиц для формирования выборочной совокупности:
1) случайный (непреднамеренный) отбор, когда выборочная совокупность образуется путем жеребьевки или с помощью таблицы случайных чисел,
2) механический отбор, когда выборочная совокупность определяется из генеральной совокупности, разбитой на равные интервалы (группы),
3) типический отбор (расслоенный, стратифицированный) с предварительным расчленением генеральной совокупности на качественно однородные типические группы (не обязательно равные),
4) серийный или гнездовой отбор, когда из генеральной совокупности отбираются не отдельные единицы, а серии, при этом внутри каждой из попавшей в выборку серии обследуются все без исключения единицы.
1.4. Статистические группировки
Одним из основных и наиболее распространенных методов обработки и анализа первичной статистической информации является группировка. Понятие статистической группировки в широком смысле слова охватывает целый комплекс статистических операций. Прежде всего, к ним относится объединение зарегистрированных при наблюдении единичных случаев в группы, сходные в том или ином отношении, поскольку целостную характеристику совокупности необходимо сочетать с характеристикой основных ее частей, классов и т.д. Результаты сводки и группировки данных статистического наблюдения представляются в виде статистических рядов распределений и таблиц.
Значение группировок состоит в том, что этот метод, во-первых, обеспечивает систематизацию и обобщение результатов наблюдения, а во-вторых, метод группировок является основой применения других методов статистического анализа основных сторон и характерных особенностей изучаемых явлений.
Цель статистической группировки состоит в разделении единиц совокупности на ряд групп для расчета и анализа обобщающих групповых показателей, которые дают возможность получить представление о составе, структуре и взаимосвязях изучаемого объекта или явления.
Обобщающие статистические показатели, характеризующие каждую выделенную группу, могут быть представлены в форме абсолютных, относительных и средних величин.
В табл. 2 сведены различные виды статистических группировок, различающиеся в зависимости от задачи группировки:
Таблица 2
| Задача группировки | Тип группировки |
| Выделение социально-экономических типов явлений | Типологическая |
| Выявление состава и структуры совокупности | Структурная |
| Установление причинно-следственных связей между причинами явлений | Факторная (аналитическая) |
Основанием группировки выступают группировочные признаки, по которым единицы изучаемой совокупности относят к определенным группам. Если группировка выполнена по одному признаку, то она считается простой,если по двум и более признакам – то комбинационной (или комбинированной).
Первичнойназывают группировку, образованную на основе первичных данных, собранных в процессе статистического наблюдения.
Вторичная группировка выполняется по данным первичной, если есть необходимость получить меньшее количество, но более крупных групп или привести в сопоставимый вид данные, сгруппированные по размеру интервалы с целью их возможного сравнения.
Классификация и характеристика признаков группировки представлена в табл. 3.
С задачами типологической группировки, которая обычно предполагает разделение неоднородной совокупности на качественно однородные группы, тесно связаны две другие задачи группировок: изучение структуры и структурных сдвигов в исследуемой однородной совокупности и выявление в ней взаимосвязи отдельных признаков изучаемого явления.
Примерами типологических группировок служить группировки хозяйственных объектов по формам собственности, разделение экономически активного населения на занятых и безработных, работников на занятых преимущественно физическим и умственным трудом.
Методология типологических группировок определяется тем, насколько ясно проявляются качественные различия изучаемых явлений. Например, при группировке отраслей промышленности по экономическому
Таблица 3
| Принцип классификации | Виды признаков | Характерные особенности |
| По содержанию (сущности) | Существенные | Выражают основное содержание изучаемых явлений |
| Второстепенные | Важные для характеристики изучаемых явлений, но не отнесенные к существенным | |
| По возможности количественного измерения | Количественные, в том числе: а) дискретные (прерывные) б) непрерывные | Отражают свойство явления, которое можно измерить Выражаются только целым числом Выражаются как целым, так и дробным числом |
| Атрибутивные (качественные), в том числе альтернативные | Признак количественно не может быть измерен и записывается в виде текста Встречаются только в двух взаимоисключающих вариантах (или – или) |
назначению продукции выделяются отрасли, производящие средства производства, и отрасли, производящие предметы потребления, в макроструктуре розничного товарооборота выделяются производственные и непроизводственные товары. В большинстве случаев качественные различия между явлениями не проступают столь отчетливо. Например, выделение в отраслях крупных, средних и мелких предприятий является достаточно сложной в методологическом отношении проблемой.
1.5. Методы обработки и анализа статистической информации
В процессе статистического наблюдения получают данные о значениях тех или иных признаков, характеризующих каждую единицу исследуемой совокупности. Для характеристики совокупности в целом или ее частей данные по отдельным единицам совокупности подвергают сводке и в результате получают обобщающие показатели, в которых отражаются результаты познания количественной стороны изучаемых явлений.
Статистическим показателем называют обобщающую количественно-качественную величину, характеризующую социально-экономические явления и процессы.
Индивидуальные значения совокупности представляют собой признаки, а количественно-качественная характеристика какого-либо свойства совокупности (группы) – статистический показатель. Например, средняя успеваемость конкретного студента – это признак, средняя успеваемость студентов вуза – показатель.
Обобщающие показатели могут быть представлены абсолютными, относительными и средними величинами, которые повсеместно используются в планировании и анализе деятельности предприятий и фирм, отраслей и экономики в целом.
Абсолютные показатели получают путем суммирования первичных данных. Они могут быть индивидуальные и общие (итоговые). Индивидуальные абсолютные величины выражают размер количественных признаков у отдельных единиц изучаемой совокупности. Общие и групповые абсолютные величины – это итоговые и групповые количественные характеристики признаков. С помощью абсолютной величины характеризуют абсолютные размеры изучаемых явлений: объем, массу, площадь, длину и др. Абсолютные показатели – это всегда именованные числа (имеют единицы измерения), которые могут быть натуральные, условно-натуральные (для сопоставления однородной, но разнокачественной продукции единицы физических величин переводят в условные единицы при помощи специальных коэффициентов) и стоимостные (денежные).
Для сравнения, сопоставления абсолютных величин между собой во времени, пространстве и прочих отношениях используются относительные величины, т.е. обобщающие показатели, выражающие количественное отношение двух абсолютных величин друг к другу.
Относительные величины могут быть результатом сопоставления:
– одноименных статистических показателей (с прошлым периодом – относительные величины динамики и планового задания; с планом – относительные величины выполнения плана; части и целого или частей между собой – относительные величины соответственно структуры и координации; в пространстве – относительные величины наглядности);
– разноименных статистических показателей (относительные величины интенсивности).
1.5.1. Метод средних величин
Средняя величина представляет собой обобщенный показатель, выражающий типичный, т.е. свойственный большинству признаков уровень. Метод средних позволяет заменить большое число варьирующих значений признака одной усредненной величиной.
Различают средние: степенные и структурные.
Формулы для расчета степенных средних представлены в табл. 4.
В табл. 4 используются следующие обозначения:  значение признака
значение признака  й единицы совокупности или
й единицы совокупности или  й вариант признака для взвешенной средней;
й вариант признака для взвешенной средней;  объем совокупности;
объем совокупности;  вес
вес  го варианта признака;
го варианта признака;  число вариантов усредняемого признака.
число вариантов усредняемого признака.
Использование невзвешенных (простых) и взвешенных средних зависит от повторяемости вариант признака:
Таблица 4
| Вид средней | Формула для расчета средней | |
| Невзвешенная | Взвешенная | |
| Средняя арифметическая | 
| 
|
| Средняя гармоническая | 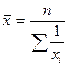
| 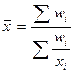
|
| Средняя геометрическая | 
| 
|
| Средняя квадратическая | 
| 
|
| Средняя кубическая | 
| 
|
– при отсутствии таких повторений или при повторении только отдельных вариант ограниченное число раз применяются невзвешенные средние;
– при повторении всех или почти всех вариант многократно применяются взвешенные средние.
Расчет средних величин используется при:
– оценке характеристики типичного уровня по данной совокупности;
– сравнении типичных уровней по двум и более совокупностям;
– расчете нормы при установлении плановых заданий, договорных обязательств.
На практике чаще всего используется среднее арифметическое. Средняя гармоническая используется в тех случаях, когда известен числитель, но неизвестен знаменатель исходного соотношения средней. В основном средняя геометрическая используется для осреднения индивидуальных показателей в динамике. Степенные средние второго и более высоких порядков применяются при расчете показателей вариации, взаимосвязи, структурных изменений, асимметрии и эксцесса.
К структурным средним относятся две основные характеристики вариационного ряда распределения – мода и медиана.
Мода – это то значение признака, которое наиболее часто встречается в данной совокупности, т.е. отражает то значение признака, которое является наиболее типичным, преобладающим, доминированным. При большом числе наблюдений совокупность может характеризоваться двумя и более модальными вариантами.
Медиана – это вариант изучаемого признака, который делит ранжированный ряд данных на две равные части: 50 % единиц исследуемой совокупности будут иметь значения признака меньше, чем медиана, а 50 % – значения признака больше, чем медиана.
При определении медианы по несгруппированным (первичным) данным сначала необходимо расположить их в возрастающем порядке (ранжировать). Затем нужно определить «позицию» медианы или определить номер той единицы, значение признака у которой будет соответствовать медиане:
 ,
,
где  число единиц в исследуемой совокупности.
число единиц в исследуемой совокупности.
1.5.2. Вариационный анализ
Вариация – это различие индивидуальных значений (изменение) признаков внутри изучаемой совокупности. Показатели вариации позволяют оценить:
- разброс значений признака у единиц статистической совокупности;
- устойчивость развития изучаемых процессов во времени;
- влияние факторного признака на изменение признака результативности;
- различного рода риски (страховой, систематический и т.д.).
Различают абсолютные и относительные показатели вариации. К абсолютным показателям вариации относятся: размах вариации  , среднее линейное отклонение
, среднее линейное отклонение  , дисперсия
, дисперсия 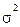 и среднее квадратическое отклонение
и среднее квадратическое отклонение  . Соотношения для расчета этих показателей сведены в табл. 5.
. Соотношения для расчета этих показателей сведены в табл. 5.
Таблица 5
| Показатели | Формулы расчета | |
| для несгруппированных данных | для сгруппированных данных | |
| Размах вариации (колебаний) | 
| |
| Среднее линейное отклонение | 
| 
|
| Дисперсия | 
| 
|
| Среднеквадратическое отклонение | 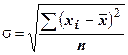
| 
|
где:  значение признака
значение признака  ;
; 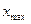 и
и  соответственно максимальное и минимальное значение признака
соответственно максимальное и минимальное значение признака 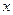 в совокупности;
в совокупности;  средняя арифметическая величина;
средняя арифметическая величина;  объем совокупности;
объем совокупности;  вес
вес  го варианта признака.
го варианта признака.
Определение размаха вариации является необходимым этапом группировки первичной статистической информации. Данный показатель вариации имеет два существенных недостатка: а) сильно зависит от максимальных аномальных значений признака и б) не учитывает «внутреннюю» вариацию между границами, определяемыми максимальным и минимальным значениями. Поэтому он не дает исчерпывающую характеристику вариации.
Показатель среднего линейного отклонения дает обобщенную характеристику степени разброса признака в совокупности, однако он реже используется по сравнению с дисперсией и средним квадратическим отклонением, так как при его расчете приходится допускать некорректные с точки зрения математики действия, нарушать законы алгебры.
Дисперсия представляется в квадратах единиц, в которых измеряется регистрируемый признак, поэтому интерпретация этого показателя довольно затруднительна. В связи с этим введен показатель среднеквадратического отклонения, который измеряется в тех же единицах измерения, что и индивидуальное значение признака.
Относительные показатели вариации рассчитываются в процентах (по отношению к средней арифметической или к медиане ряда). В статистике используются следующие относительные показатели вариации:
1) коэффициент осцилляции

показывает относительный разброс крайних значений признаков вокруг средней арифметической;
2) относительное линейное отклонение

характеризует долю усредненного значения абсолютных отклонений от средней арифметической;
3) коэффициент вариации
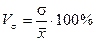
наиболее часто применяется, так как характеризует степень однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
1.5.3. Корреляционный анализ
Важнейшая задача общей теории статистики состоит в исследовании объективно существующих связей между явлениями. В процессе статистического исследования выясняются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов.
В статистике различают функциональную связь и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Такая связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности.
Если причинная связь проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая связь называется стохастической. Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков. Признаки первой группы называют факторными, а признаки, которые являются результатом влияния этих факторов, – результативными.
В статистике не всегда требуются количественные оценки связи, часто важно определить лишь ее направление и характер, выявить форму воздействия одних факторов на другие. Одним из основных методов выявления наличия связи является корреляционный метод, который имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
В статистике различаются следующие варианты зависимостей:
1) парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными);
2) частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
3) множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
Основным методом выявления наличия корреляционной связи является метод аналитической группировки и определении групповых средних. Он заключается в том, что все единицы совокупности разбиваются на группы по величине факторного признака и для каждой группы определяется средняя величина результативного признака.
Теснота связи количественно выражается величиной коэффициента корреляции; наиболее распространенные из них сведем в табл. 6:
Таблица 6
| Вид связи (зависимости) | Показатель тесноты связи | Расчетная формула |
| Парная линейная | Линейный коэффициент корреляции  по несгруппированным данным по несгруппированным данным
| 
|
| Произвольная форма (линейная и криволинейная) | Эмпирическое корреляционное отношение 
| 
|
Совокупное влияние факторных признаков 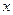 на результативный признак на результативный признак 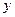
| Коэффициент множественной (совокупной) корреляции 
| 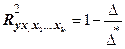
|
Связь между результативным признаком 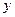 и каждым из факторных признаков при исключении влияния других факторных признаков и каждым из факторных признаков при исключении влияния других факторных признаков
| Частный коэффициент корреляции
 
| 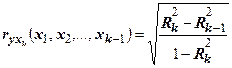
|
В табл. 6 используются следующие обозначения:
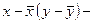 отклонение вариантов значений соответственно факторного и результативного признаков от их средних величин;
отклонение вариантов значений соответственно факторного и результативного признаков от их средних величин;
 число единиц совокупности;
число единиц совокупности;
 среднее квадратическое отклонение соответственно факторного и результативного признаков;
среднее квадратическое отклонение соответственно факторного и результативного признаков;
 и
и  соответственно общая дисперсия и средняя внутригрупповая дисперсия результативного признака соответственно, где:
соответственно общая дисперсия и средняя внутригрупповая дисперсия результативного признака соответственно, где:  общая средняя для всей совокупности;
общая средняя для всей совокупности;  число единиц в соответствующих группах;
число единиц в соответствующих группах;  внутригрупповая дисперсия;
внутригрупповая дисперсия;  матрица парных коэффициентов корреляции:
матрица парных коэффициентов корреляции:
| Признак | 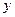
| 
| 
| 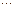
| 
|
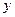
| 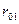
| 
| 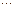
| 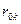
| |

| 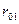
| 
| 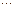
| 
| |

| 
| 
| 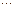
| 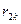
| |
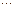
| 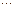
| 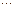
| 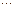
| 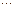
| 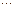
|

| 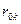
| 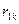
| 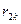
| 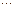
|
 матрица парных коэффициентов корреляции без верхней строки и первого столбца;
матрица парных коэффициентов корреляции без верхней строки и первого столбца;
 (
(  ) – коэффициент детерминации результативного признака
) – коэффициент детерминации результативного признака 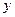 с набором факторных признаков
с набором факторных признаков  (
(  ) соответственно, равный квадрату коэффициента множественной корреляции
) соответственно, равный квадрату коэффициента множественной корреляции  .
.
Большинство коэффициентов, применяемых для оценки силы (тесноты) связи, могут принимать значения (по абсолютной величине) от 0 до 1. Шкала значений коэффициентов связи с указанием их интерпретации представлена на табл. 7.
Таблица 7
| Значение коэффициента связи | Сила связи |
До 
| Практически отсутствует |

| Слабая |

| Средняя |

| Сильная |
1.5.4. Индексный анализ
Индекс – это относительный показатель, характеризующий среднее изменение во времени, в пространстве, по сравнению с планом или нормативом общественного явления, элементы которого не поддаются непосредственному суммированию. Классификация индексов представлена в табл. 8.
В теории индексного метода используются следующие понятия и обозначения:
– индексный набор – перечень элементов, включаемых в расчет индекса;
– индексируемая величина – значение признака, изменение которого изучается. При построении индексов индексируемая величина всегда является переменной. Каждая индексируемая величина имеет свое обозначение:
 цена единицы продукции,
цена единицы продукции,
 себестоимость одного изделия;
себестоимость одного изделия;
 физический объем продукции,
физический объем продукции,
 объем продукции в стоимостном выражении,
объем продукции в стоимостном выражении,
 затраты на производство продукции,
затраты на производство продукции,
 затраты времени (численность работающих),
затраты времени (численность работающих),
 выработка продукции,
выработка продукции,
 трудоемкость продукции;
трудоемкость продукции;
Таблица 8
| Признаки классификации | Виды индексов |
| 1. По характеру индексируемых явлений | а) цен, б) производительности труда, в) физического объема продукции, г) себестоимости единицы продукции |
| 2. В зависимости от охвата индексируемых явлений | а) индивидуальные, б) общие (агрегатные и средние), в) групповые |
| 3. По форме и методам вычисления | а) агрегатные, б) средние арифметические и гармонические, тождественные агрегатному, в) средних величин (переменного, постоянного состава и структурных сдвигов) |
| 4. В зависимости от выбора весов | а) с постоянными весами, б) с постоянными весами |
| 5. В зависимости от базы сравнения | а) базисные, б) цепные, в) территориальные, г) плановые |
– веса-соизмерители – показатели, являющиеся условно-постоянной величиной при построении индексов.
Уровни базисного периода обозначаются подстрочным символом 0, отчетного – 1.
К задачам, решаемым с помощью индексного метода, относятся:
1) изучение динамики, т.е. изменения явлений во времени (индексы динамики),
2) изучение влияния отдельных факторов на динамику сложных экономических явлений (факторные индексы),
3) характеристика выполнения плановых заданий, договорных обязательств (плановые индексы),
4) сравнение явлений, относящихся к одному и тому же периоду времени, но разным территориям (территориальные индексы),
5) определение влияния структурных сдвигов (индексы структурных сдвигов) и др.
Основные виды индексов представлены в табл. 9.
Индивидуальные (частные) индексы характеризуют изменение отдельных единиц статистической совокупности.
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих изучаемую совокупность. Могут рассчитываться в агрегатной и средней формах.
Таблица 9
Сводная таблица индексов
| Индексы | ||||
| Цен | Физического объема | Себестоимости | Производительности труда | |
| выработки | трудоемкости | |||
| Индивидуальные | ||||

| 
| 
| 
| 
|
| Агрегатные | ||||
Ласпейреса

| 
| 
| 
| 
|
Пааше

| 
| 
| 
| 
|
Лоу

| 
| 
| ||
| Средние арифметические | ||||

| 
| 
| 
| 
|
| Средние гармонические | ||||

| 
| 
| 
| 
|
| Переменного состава | ||||

| 
| 
| 
| |
| Постоянного состава | ||||

| 
| 
| 
| |
| Структурных сдвигов | ||||

| 
| 
| 
|
Сущность агрегатного индекса в том, что несоизмеримые элементы индексного набора приводятся к соизмеримому виду путем из взвешивания (умножения) на соизмерители-веса и дальнейшего суммирования по всем элементам индексного набора. Соизмерители необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям. Соизмерители остаются постоянными на одном уровне (текущего или базисного периода). Таким образом, на величине агрегатного индекса сказывается влияние только фактора, который определяет изменение индексируемой величины.
Общие индексы могут быть представлены другим способом – путем вычисления средней величины из индивидуальных индексов. Значения общих индексов, рассчитанных по агрегатному способу и путем вычисления средней величины из индивидуальных индексов, будут одинаковыми.
В качестве примера рассмотрим две средние формы средних индексов физического объема продукции: среднюю арифметическую и среднюю гармоническую формы.
Первая форма (называемая средним арифметическим индекса, тождественного агрегатному)

получается подстановкой в числитель агрегатного индекса

соотношения  , эквивалентного индивидуальному индексу
, эквивалентного индивидуальному индексу  .
.
Вторая форма (называемая средним гармоническим индекса, тождественного агрегатному)

получается подстановкой в знаменатель агрегатного индекса

соотношения  , эквивалентного индивидуальному индексу
, эквивалентного индивидуальному индексу  .
.
Индексы динамики среднего уровня рассчитываются по различным качественным показателям. Например, для средней цены можно рассчитать:
а) индекс переменного состава:
 ,
,
где  и
и  – удельный вес продукции
– удельный вес продукции  го предприятия в общем объеме произведенной продукции по группе предприятий соответственно в отчетном и базисном периодах.
го предприятия в общем объеме произведенной продукции по группе предприятий соответственно в отчетном и базисном периодах.
Этот индекс отражает изменение как среднего признака (в данном случае – цены), так и структуры совокупности (производства продукции). На его основе могут быть построены:
б) индекс постоянного состава, отражающий изменение средней цены в результате изменения индивидуальных цен при условии постоянства структуры совокупности (т.е. значения показателя, принимаемого в качестве весов, остаются неизменными на уровне отчетного периода):
 ;
;
в) индекс структурных сдвигов, отражающий изменение средней цены в результате изменения структуры совокупности при условии постоянства цен на продукцию:
 .
.
1.5.5. Анализ рядов динамики
Рядом динамики называют числовые значения статистического показателя, представленные во временнόй последовательности. Он состоит из двух граф: в первой указываются периоды (или даты), во второй – показатели, характеризующие изучаемый объект за эти периоды (или на эти даты) и называемые уровнями ряда.
Различают интервальные и моментные ряды динамики. В интервальном ряду приводятся данные, характеризующие величину показателя за определенные периоды (сутки, месяц, квартал, год и т.д.). Особенностью интервальных рядов из абсолютных величин является то, что их уровни можно суммировать, получая новые численные значения объема явления, относящиеся к более длительным периодам.
В моментном ряду динамики приводятся данные, характеризующие размеры явления на определенные моменты (даты) времени. Суммирование уровней моментных динамических рядов лишено смысла, так как каждый последующий уровень полностью или частично включает в себя предыдущий уровень. Однако разность уровней имеет смысл, характеризуя увеличение или уменьшение уровня ряда между датами учета.
При формировании рядов динамики уровни ряда должны быть сопоставимыми, т.е. для всех периодов или дат все уровни должны быть представлены не только в одинаковых, но и в равноценных единицах измерения и притом с одинаковой полнотой охвата для различных частей явления, представленного рядом динамики. В интервальных рядах уровни показателей должны относиться к периодам с одинаковой продолжительностью, для моментных – должна соблюдаться неизменность даты учета (например, наличие материалов на складе на первое число каждого месяца или квартала).
Перед анализом ряда динамики необходимо, исходя из цели исследования, обеспечить сопоставимость уровней ряда дополнительными расчетами, т.е. произвести так называемое смыкание рядов динамики.
Специальным условием сопоставимости абсолютных величин интервального динамического ряда является равенство периодов, за которые приводятся данные; если это условие нарушено, то ряд подвергают дополнительной обработке – рассчитывают величины явления в среднем на единицу времени.
При изучении рядов динамики перед статистикой стоят следующие задачи:
1) охарактеризовать интенсивность развития явления от периода к периоду (от даты к дате), а также среднюю интенсивность развития за исследуемый период;
2) выявить основную тенденцию в развитии явления;
3) осуществить прогноз развития на будущее, а также изучить сезонные колебания.
Для изучения интенсивности изменения уровней ряда во времени исчисляются следующие показатели динамики: абсолютные приросты, коэффициенты роста, темпы роста, темпы прироста, абсолютные значения одного процента прироста.
Перечисленные показатели динамики можно исчислять с переменной или постоянной базой. Если производится сравнение каждого уровня с предыдущим уровнем, то получаются показатели динамики с переменной базой (цепные показатели динамики). Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым за базу сравнения, то получаются показатели динамики с постоянной базой (базисные показатели динамики). База сравнения должна выбираться обоснованно, в зависимости от экономических особенностей явления и задач исследования.
Для расчета показателей динамики приняты следующие обозначения:
 уровень любого периода (кроме первого), называемый уровнем текущего периода;
уровень любого периода (кроме первого), называемый уровнем текущего периода;
 уровень периода, предшествующего текущему;
уровень периода, предшествующего текущему;
 уровень, принятый за постоянную базу сравнения (часто начальный уровень).
уровень, принятый за постоянную базу сравнения (часто начальный уровень).
Методы расчета показателей динамики представлены в табл. 10 (одинаковы для моментных и для интервальных рядов).
Абсолютный прирост показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного.
Коэффициент роста показывает, во сколько раз уровень текущего периода больше (меньше) базисного.
Таблица 10
| Показатель | Метод расчета | |
| с переменной базой (цепные) | с постоянной базой (базисные) | |
| 1. Абсолютный прирост (Δ) | 
| 
|
2. Коэффициент роста (  ) )
| 
| 
|
3. Темп роста (  ), % ), %
| 
| 
|
4. Темп прироста (  ), % ), %
| 


| 


|
| 5. Абсолютное значение 1 % прироста (А) |  ; ; 
|  ; ; 
|
Темп роста – это коэффициент роста, выраженный в процентах; он показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периода.
Абсолютное значение 1% прироста показывает, какая абсолютная величина скрывается за относительным показателем – одним процентом прироста.
Между базисными и цепными абсолютными показателями существует взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики.
Взаимосвязь между базисными и цепными коэффициентами роста такова: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста, а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему коэффициенту роста.
Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики; метод их расчета представлен в табл. 11.
Средние показатели динамики исчисляются одинаковым методом для интервальных и моментных рядов, исключение составляет лишь расчет среднего уровня ряда.
В приведенных формулах используются следующие обозначения:
 все уровни последовательных периодов (дат);
все уровни последовательных периодов (дат);
 число уровней ряда;
число уровней ряда;
 продолжительность периода, в течение которого уровень не изменяется.
продолжительность периода, в течение которого уровень не изменяется.
При статистическом анализе и сопоставлении стохастически взаимосвязанных рядов динамики, характеризующих различные социально-
Таблица 11
Средние показатели динамики
| Показатель | Метод расчета |
1. Средний уровень ряда  :
а) для интервального ряда
б) для моментного ряда с равными интервалами
в) для моментного ряда с неравными интервалами :
а) для интервального ряда
б) для моментного ряда с равными интервалами
в) для моментного ряда с неравными интервалами
|



|
2. Средний абсолютный прирост 
|  или или 
|
3. Средний коэффициент роста 
|  или или
 ; ;  ; ;
|
4. Средний темп роста  , % , %
| 
|
5. Средний темп прироста  , % , %
|  или или 
|
6. Средняя величина абсолютного значения 1% прироста 
| 
|
экономические явления, рассчитывают коэффициент опережения. Он показывает, во сколько раз один ряд динамики растет быстрее другого, и определяется сопоставлением коэффициентов роста двух рядов. Коэффициенты опережения можно также определить путем сопоставления темпов прироста:
 ;
;  ,
,
где:
 больший коэффициент роста;
больший коэффициент роста;
 меньший коэффициент роста;
меньший коэффициент роста;
 больший темп прироста;
больший темп прироста;
 меньший темп прироста.
меньший темп прироста.
Несопоставимость уровней может иметь место по следующим причинам:
1) изменение круга включенных в совокупность объектов;
2) различное понимание единицы совокупности;
3) территориальные изменения;
4) различия в единицах измерения;
5) изменение методологии расчета уровней;
6) изменение критического момента регистрации;
7) структурные изменения в совокупности.
При несопоставимости уровней по той или иной причине временной ряд может быть приведен к сопоставимому виду на основе коэффициента пересчета или путем перехода к относительным показателям.
Для определения среднего уровня ряда динамики за рассматриваемый временной интервал используется одна из формул табл. 12:
Таблица 12