В. Метод частных производных

Приращение функции всегда можно выразить через приращение аргумента, используя определение частной производной. Частной производной функции называют производную этой функции по соответствующему аргументу, когда остальные аргументы считаются фиксированными. В данном случае под функцией понимается рассчитываемая величина А, а под независимыми переменными - измеряемые величины a, b, c. Тогда, ограничиваясь членами первого порядка малости выражение (10) можно переписать так:

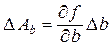; ; . (11)

Отметим, что производные , , рассчитываются при средних значениях .

Полная погрешность DА получается путем подстановки выражений (11) в формулу (9):

. (12)

Этот метод расчета применяется, если выражения производных значительно проще, чем сама функция (например, если расчетная формула представляет сумму слагаемых, являющихся громоздкими выражениями).