Нахождение табличных интегралов
(интегрирование по формулам)
Пример 1. Найти 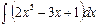 .
.
Решение. Это интеграл от алгебраической суммы. Применяя сначала свойства 2 и 3, а затем формулу (3) табличных интегралов, получим:

Пример 2. Найти 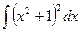 .
.
Решение. Применим формулу сокращённого умножения (квадрата суммы) и свойства 2 и 3:

Пример 3. Найти 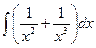 .
.
Решение. Воспользуемся формулой: 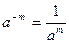 :
:

Пример 4. Найти  .
.
Решение. Представим данный интеграл в виде суммы двух интегралов; для этого каждое слагаемое числителя делим на знаменатель подынтегральной функции:

Пример 5. Найти 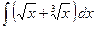 .
.
Решение. Воспользуемся формулой перехода к дробному показателю:  :
:
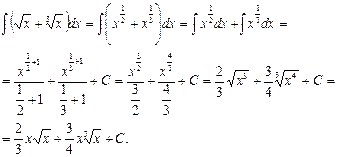
Пример 6. 
 Пример 7.
Пример 7. 

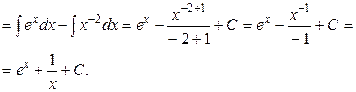
Пример 8. Найти  .
.
Решение. Перепишем интеграл в виде:
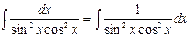
числитель подынтегральной функции, то есть единицу, запишем в виде тригонометрического тождества: 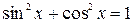 . Таким образом,
. Таким образом,
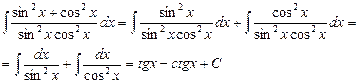
Пример 9. 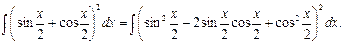
Используем формулы понижения степени и двойного угла:

Получим:


Пример 10. Найти  .
.
Решение. В числителе подынтегральной функции осуществим следующее тождественное преобразование: прибавим и отнимем единицу; затем разложим интеграл на сумму 2-х интегралов:
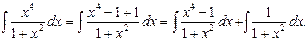
К числителю первого интеграла применим формулу разности квадратов, а второй вычислим по формуле (13):

Пример 11. Найти интеграл 
Решение. Запишем числитель в виде
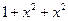
почленно разделим числитель на знаменатель, получим сумму двух табличных интегралов:

Пример 12. Найти интеграл: 
Решение. В соответствие с формулой  , преобразуем знаменатель, а затем, разделив почленно числитель на знаменатель, сведем данный интеграл к сумме двух табличных интегралов:
, преобразуем знаменатель, а затем, разделив почленно числитель на знаменатель, сведем данный интеграл к сумме двух табличных интегралов:
