Шифрование методом замены (подстановки)

Шифр подстановки – это метод шифрования, в котором элементы исходного открытого текста заменяются зашифрованным текстом в соответствии с некоторым правилом. Элементами текста могут быть отдельные символы (самый распространённый случай), пары букв, тройки букв, комбинирование этих случаев и так далее. В классической криптографии различают четыре типа шифра подстановки[8]:

• Одноалфавитный шифр подстановки (шифр простой замены) — шифр, при котором каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита.
• Однозвучный шифр подстановки похож на одноалфавитный за исключением того, что символ открытого текста может быть заменен одним из нескольких возможных символов.
• Полиграммный шифр подстановки заменяет не один символ, а целую группу. Примеры: шифр Плейфера, шифр Хилла.
• Полиалфавитный шифр подстановки состоит из нескольких шифров простой замены. Примеры: шифр Виженера, шифр Бофора, одноразовый блокнот.

В качестве альтернативы шифрам подстановки можно рассматривать перестановочные шифры. В них, элементы текста переставляются в ином от исходного порядке, а сами элементы остаются неизменными. Напротив, в шифрах подстановки, элементы текста не меняют свою последовательность, а изменяются сами.

Шифры простой замены

В шифрах простой замены замена производится только над одним-единственным символом. Для наглядной демонстрации шифра простой замены достаточно выписать под заданным алфавитом тот же алфавит, но в другом порядке или, например, со смещением. Записанный таким образом алфавит называют алфавитом замены.

Шифр простой замены Атбаш[9], использованный для еврейского алфавита и получивший оттуда свое название. Шифрование происходит заменой первой буквы алфавита на последнюю, второй на предпоследнюю и т.д. Шифр Атбаш для английского алфавита:

Исходный алфавит:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Алфавит замены:	Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

 

Шифр Цезаря — один из древнейших шифров. При шифровании каждая буква заменяется другой, отстоящей от ней в алфавите на фиксированное число позиций. Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки.

Общая формула шифра Цезаря имеет следующий вид:

С=P+K (mod M),

(4.1)

 

где P – номер символа открытого текста, С – соответствующий ему номер символа шифротекста, K – ключ шифрования (коэффициент сдвига), M – размер алфавита (для русского языка M = 32)

Для данного шифра замены можно задать фиксированную таблицу подстановок, содержащую соответствующие пары букв открытого текста и шифротекста.

Пример 4.1. Таблица подстановок для символов русского текста при ключе K=3 представлена в таблице 4.1. Данной таблице соответствует формула:

С=P+3 (mod 32)

(4.2)

 

Табл. 4.1. Табл. подстановок шифра Цезаря для ключа K=3

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

А

Б

В

 

Согласно формуле (4.2) открытый текст «БАГАЖ» будет преобразован в шифротекст «ДГЖГЙ».

Дешифрование закрытого текста, зашифрованного методом Цезаря согласно (4.1), осуществляется по формуле:

 

P=C-K (mod M)

(4.3)

 

Естественным развитием шифра Цезаря стал шифр Виженера. Например, шифрование с использованием ключа будет иметь результат:

Исходный алфавит:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Алфавит замены:	E F G H I J K L M N O P Q R S T U V W X Y Z A B C D

Современным примером шифра Цезаря является ROT13. Он сдвигает каждый символ английского алфавита на 13 позиций. Используется в интернет-форумах, как средство для сокрытия основных мыслей, решений загадок и пр. [9].

 

Шифр с использованием кодового словаявляется одним из самых простых как в реализации, так и в расшифровывании. Идея заключается в том, что выбирается кодовое слово, которое пишется впереди, затем выписываются остальные буквы алфавита в своем порядке. Шифр с использованием кодового слова WORD.

Исходный алфавит:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Алфавит замены:	W O R D A B C E F G H I J K L M N P Q S T U V X Y Z

Как мы видим, при использовании короткого кодового слова мы получаем очень и очень простую замену. Также мы не можем использовать в качестве кодового слова слова с повторяющимися буквами, так как это приведет к неоднозначности расшифровки, то есть двум различным буквам исходного алфавита будет соответствовать одна и та же буква шифрованного текста. Слово COD будет преобразованно в слово RLD [10].

Шифр простой моноалфавитной замены является обобщением шифра Цезаря и выполняет шифрование по следующей схеме:

 

,

(4.4)

 

где - ключ шифрования, наибольший общий делитель .

Пример 4.2.

Пусть M=26, a=3, K=6, НОД(3,26) = 1. Тогда получаем следующую таблицу подстановок для шифра простой моноалфавитной замены.

 

Табл. 4.2. Табл. подстановок для шифра моноалфавитной замены.

A

B

C

D

E

F

G

H

I

G

K

L

M

N

O

P

Q

R

S

P

C

T

U

V

W

X

Y

Z

P

C

 

Тогда открытый текст «HOME» будет преобразован в шифротекст «BWQS».

Дешифрование текста «BWQS» выполняем в порядке обратном шифрованию, т.е. смотрим у буквы В ее номер Р обозначим его через . Он равен 1. Складываем с числом М равным 26. Получим 27. Отнимаем К равное 6. Получаем 21. Делим на 3. Получаем число 7. Именно под этим номером стоит в исходном тексте буква Н. Аналогичные действия выполняются и над оставшимися буквами. Получаем расшифрованное слово «HOME». То есть формула дешифровки выглядит следующим образом:

 

(4.5)

Шифр Гронсфельда. Данный шифр представляет собой модификацию шифра Цезаря с числовым ключом. При реализации данного шифра под буквами исходного сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Получение символа шифротекста осуществляют также, как это делается в шифре Цезаря, при этом смещение символа открытого текста производят на количество позиций, соответствующего цифре ключа, стоящей под ним.

 

Пример 4.3.

Пусть необходимо зашифровать исходное сообщение «НОЧЕВАЛА ТУЧКА ЗОЛОТАЯ», в качестве ключа возьмем К=193431.

 

Табл. 4.3. Табл. подстановок шифра Гронсфельда для ключа K=193431

Сообщение

Н

О

Ч

Е

В

А

Л

А

Т

У

Ч

К

А

З

О

Л

О

Т

А

Я

Ключ

Шифро- текст

О

Ч

Ь

Й

Е

Б

М

Й

Х

Ч

Ь

Л

Б

Р

С

П

С

У

Б

И

 

Для того, чтобы зашифровать первую букву сообщения Н, необходимо сдвинуть ее в алфавите русских букв на число позиций, соответствующее цифре ключа, т.е. на 1, в результате чего получим букву О.

Дешифрование шифротекста предполагает сдвиг его символов на необходимое число позиций в обратную сторону.

 

Шифрование методом Вернама

При шифровании открытого текста, каждый его символ представляется в двоичном виде [3]. Ключ шифрования также представляется в двоичной форме. Шифрование исходного текста осуществляется путем сложения по модулю 2 двоичных символов открытого текста с двоичными символами ключа:

Y=PÅK

(4.6)

Дешифрование состоит в сложении по модулю 2 символов шифротекста с ключом.

 

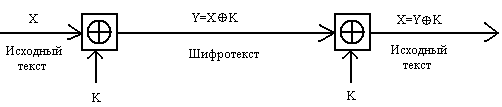
Рис. 4.2. Схема системы шифрования Вернама

 

Модификация системы шифрования Вернама используется для криптографической защиты информации в архиваторе ARJ. Формула (4.6) в этом случае принимает следующий вид:

Y=PÅ(K+VALUE),

(4.7)

где VALUE – фиксированное значение.

Пример 4.4. Зашифруем с помощью системы Вернама открытый текст «БЛАНК» с помощью ключа «ОХ».

Преобразуем открытый текст «БЛАНК» в ASCII коды: Б=129, Л=139, A=128, Н=141, К=138. В двоичном виде последовательность 129, 139, 128, 141, 138 представится в виде 10000001 10001011 10000000 10001101 10001010.

 

Табл. 4.4. Двоичные коды слова БЛАНК

символ	код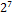
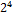
Б
Л
А
Н
К

 

Преобразуем ключ «ОХ» в ASCII коды: О=142, Х=149. В двоичном виде последовательность 142, 149 представится в виде 10001110 10010101.

Подпишем циклически ключ под открытым текстом и выполним сложение по модулю 2 соответствующих битов.

 

Табл. 4.5. Шифрование по схеме Вернама

Открытый текст
Ключ									1	0	0	1	0	1	0	1
Закрытый текст

 

Продолжение таблицы

Открытый текст
Ключ					1	0	0	1	0	1	0	1
Закрытый текст