Понятие несовершенной скважины и их виды. Приток однородной жидкости к несовершенным скважинам. Приведённый радиус скважины. Коэффициент несовершенства.

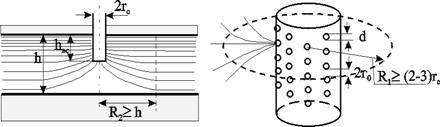
а b Рис. 3.9. Схема притока к несовершенной скважине: а - по степени вскрытия; b - по характеру вскрытия

Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной мощностью отсутствует радиальность потока по причине, обусловленной конструкцией забоя или фильтра.

Различают два вида несовершенства скважин - несовершенство по степени вскрытия и несовершенство по характеру вскрытия.

Несовершенная скважина по степени вскрытия - это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рис.3.9,а).

Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рис. 3.9,b).

На практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта.

Дебит G несовершенной скважины чаще всего меньше дебита Gс совершенной, действующей в тех же условиях, что и данная несовершенная скважина. В некоторых случаях (при торпедной или кумулятивной перфорации, когда глубина прострела достаточно велика) может наблюдаться обратная картина. Отношение данных дебитов d характеризует степень несовершенства скважины и называется параметром несовершенства

. (3.63)

Параметр несовершенства зависит от:

* относительного вскрытия пласта , (3.64)

где hвс - глубина погружения скважины в пласт , h - толщина пласта;

* плотности перфорации (числа отверстий, приходящихся на 1м фильтра), размеров и формы отверстий;

* глубины прострела.

При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины

, (3.65)

где rC – радиус несовершенной скважины, С – коэффициент несовершенства.

Приведенный радиус - это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.

Таким образом, вначале находятся приведённые радиусы rпр и дальнейший расчет несовершенных скважин ведется как для совершенных скважин радиуса rпр.

Таким образом, дебит несовершенной скважины можно определить, если известен параметр несовершенства d или приведённый радиус rпр , а также известна соответствующая формула дебита совершенной скважины. Влияние несовершенства скважины на приток при существовании закона фильтрации Дарси можно учесть величиной коэффициента С, основываясь на электрической аналогии. Согласно данной аналогии различие в дебитах совершенной Gc и несовершенной G скважин объясняется наличием добавочного фильтрационного сопротивления несовершенной скважины величиной С/2ph, т.е. дебит несовершенной скважины можно представить в виде:

. (3.66)

Учитывая (4.40), получаем зависимость между коэффициентом d и и величиной С:

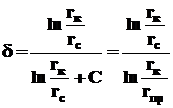. (3.67)

Влияние различного вида несовершенства скважины на приток изучалось как теоретически, так и экспериментально.

10 Общие положения неустановившегося движения упругой жидкости в деформируемой пористой среде. Уравнение пьезопроводности.

Важнейшими параметрами теории упругого режима являются коэффициенты объёмной упругости жидкости и пласта.

Коэффициент объёмной упругости жидкости bж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу

, (4.1)

где tж - объём жидкости; знак минус указывает на то, что объём tж увеличивается с уменьшением давления; bж нефти находится в пределах (7-30)10-10м2/н; bж воды находится в пределах (2,7-5)10-10м2/н.

Коэффициент объёмной упругости пласта определяется по формуле

, (4.2)

где tп - объём пласта; m - пористость; bС слабо и сильно сцементированных горных пород находится в пределах (0,3-2)10-10м2/н.

Считаем, что течение происходит по закону Дарси, и уравнение состояния упругой жидкости в линеаризованной постановке, которое получим из соотношения (2.27) разложением экспоненты в ряд Тейлора, имеет вид

, (4.8)

а также изменение пористости в зависимости от давления, полученное линеаризацией соотношения (2.34), описывается зависимостью

. (4.9)

Из (4.9) и очевидного соотношения имеем следующее дифференциальное уравнение для пористости, при пренебрежении членом, содержащим произведение bжbс

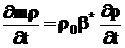. (4.10)

В то же время из общего уравнения фильтрации (2.8) .

Приравнивая правые части, с учетом выражения для потенциала , и пренебрегая членом, содержащим (р-р0)2, получим

. (4.11)

Уравнение типа (4.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент k характеризует быстроту распределения давления в пласте и носит название коэффициент пьезопроводности. Само уравнение (4.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.

11 Одномерный установившийся поток жидкости и газа в пористой среде в плоско-параллельном случае. Приток к дренажной системе.
Одномерный установившийся поток жидкости и газа в пористой среде в плоскорадиальном случае. Приток к дренажной галерее

Плоскорадиальный фильтрационный поток. Предположим, что имеется горизонтальный пласт постоянной толщины h и неограниченной или ограниченной протяженности. В пласте пробурена одна скважина, вскрывшая его на всю толщину и имеющая открытый забой. При отборе жидкости или газа их частицы будут двигаться по горизонтальным траекториям, радиально сходящимся к скважине. Такой фильтрационный поток называется плоскорадиальным. Картина линий тока в любой горизонтальной плоскости будет одинакова, и для полной характеристики потока достаточно изучить движение флюида в одной горизонтальной плоскости. В плоскорадиальном одномерном потоке давление и скорость фильтрации в любой точке зависят только от расстояния r данной точки от оси скважины.

а) б)

Рисунок 1.3: Схема плоскорадиального потока в круговом пласте: a) Общий вид; б) план.

Рисунок 1.4. Вертикальное сечение радиально - сферического фильтрационного потока

На рисунке 1.3, а, б приведена схема плоскорадиального фильтрационного потока. Схематизируемый пласт ограничен цилиндрической поверхностью радиусом Rk, (контуром питания), на которой давление постоянно и равно р_к; на цилиндрической поверхности скважины радиусом r_c (забой скважины) давление равно р_с. Кровля и подошва пласта непроницаемы. На рисунке 1.3 б, приведены сечение пласта горизонтальной плоскостью и радиальные линии тока, направленные к скважине. Если скважина не добывающая, а нагнетательная, то направление линий тока надо изменить на противоположное. Радиально - сферический фильтрационный поток. Рассмотрим схему пласта неограниченной толщины с плоской горизонтальной непроницаемой кровлей. Скважина сообщается с пластом, имеющим форму полусферы радиусом Rk, (рисунок 1.4). При эксплуатации такой скважины траектории движения всех частиц жидкости или газа в пласте будут прямолинейными в пространстве и радиально сходящимися в центре полусферического забоя, в точке О. В таком установившемся потоке давление и скорость в любой его точке будут функцией только расстояния г этой точки от центра полусферы. Следовательно, этот фильтрационный поток является также одномерным и называется радиально-сферическим.

Перейдем от координаты s к координате r, отсчитываемой от центра скважины. Для добывающей скважины s = R_к- r, так что ds= -dr; площадь фильтрационной поверхности ω(s) = 2πrh – боковая поверхность цилиндра; на контуре питания r₁=R_k, P₁=P_k на забое скважины r₂ =r_c, P₂=P_k . Тогда

Из (2.10)

(2.20)

Из (2.12)

, (2.21)

Из (2.14)

. (2.22)