Если статическая характе-ристика системы или элемента нелинейная, то система или эле-мент называются нелинейными

(рис. 8.6, б), и её поведение опреде-ляется нелинейным алгебраическим уравнением. Например, уравнение статики релейного звена (рис. 8.6, )

б) запишется в следующем виде:

В неравновесном режиме, возникающем под действием возмуще­ний и регулирующих воздействий, поведение системы описывается уравнениями динамики y(х) = f(x,x) или динамическими характери­стиками, которые определяют зависимость изменения выходной величины во времени от изменения входной величины. Динамические характеристики АСР или элемента могут быть представлены в виде дифференциальных уравнений, передаточных и переходных функций и в виде частотных характеристик.

Динамические характеристики линейных АСР описываются обык­новенными дифференциальными уравнениями вида

где a₀, a₁,..., a_n, b₀, b₁,...,b_m - постоянные коэффициенты; т - вре­мя; n - порядок левой части уравнения; m - порядок правой части урав­нения; y - изменение выходной величины; x - известное входное воз­действие.

В соответствии с условием физической реализуемости систем по­рядок правой части уравнения не должен превышать порядок левой час­ти, или m <n.

При x=0 уравнение (8.4) преобразуется в однородное уравнение

которое описывает поведение системы после снятия входного воздейст­вия, или свободное движение системы, поэтому уравнение (8.5) назы­вают уравнением свободного движения системы.

Уравнение статики (8.2) можно получить из уравнения динами­ки (8.4), приравняв все производные нулю:

Абсолютное количество реальных систем и элементов являются нелинейными, поэтому их динамические характеристики описываются нелинейными дифференциальными уравнениями, которые решаются чаще всего только численными методами. Во многих случаях можно нелинейное уравнение заменить приближенным линейным уравнением, полученным в результате линеаризации нелинейного уравнения. Воз­можность применения процедуры линеаризации нелинейных диффе­ренциальных уравнений на основе понятия малого отклонения пара­метра была доказана еще Вышнеградским.

Если нелинейность системы возникает из-за нелинейности стати­ческой характеристики, то последнюю можно линеаризовать, используя разложение нелинейной функции в ряд Тейлора с последующим отбра­сыванием нелинейных членов разложения и переходом от полных па­раметров к их отклонениям от стационарного состояния (y ₀,x₀). Нели­нейная статическая характеристика должна относиться к классу непре­рывно дифференцируемых функций.

Рассмотрим примеры построения математических моделей элемен­тов АСР и линеаризации нелинейных статических характеристик.

Построение математических моделей элементов АСР базируется на использовании закона сохранения в статике и динамике.

В статике количество выходящего из элемента вещества или энер­гии (приток) равно количеству входящего вещества или энергии (сток):

Q_ст,0 =Q_пр,0. (8.7)

В динамике разница между количеством входящего в элемент ве­щества или энергии и количеством выходящего вещества или энергии идет на накопление вещества или энергии в элементе:

Q _пр (τ)dτ- Q_ст (τ ) d τ = dQ(τ), (8.8)

Или

где dQ(x)/dx - скорость накопления вещества или энергии в элементе.

Перед построением математической модели, при необходимости, формулируются допущения. Это позволяет упростить исходную модель за счет исключения второстепенных факторов, мало влияющих на про­цесс.

Пример 1.Построить линейную математическую модель динами­ки сосуда со свободным сливом (рис. 8.7). В сосуд, находящийся под атмосферным

давлением, втекает жидкость Q_пр (входное воз­действие). Под действием гидростатического давления столба жидкости H она вытекает (Q_ст)

через отверстие, находящееся на уровне дна сосуда. Регулируемый (выходной) параметр - уровень жидкости H в сосуде. Сделаем очевидное

со свободным сливом допущение: площадь поперечного сечения S со­суда постоянна по высоте. Тогда объем жидко­сти V = Q, находящейся в сосуде, можно выразить через регулируемый

параметр

V = Q = SH. (8.10)

В состоянии равновесия приток и сток жидкости равны:

Для определения количества вытекающей жидкости воспользуемся формулой (5.7):

где S₀ - площадь сечения отверстия, через которое истекает жидкость; P₁ = H₀pg - гидростатическое давление столба жидкости, соответст­вующее стационарному значению уровня жидкости H₀; P₂= 0, так как

сосуд находится под атмосферным давлением. Тогда выражение (8.12) примет вид

где р = aS₀-j2g - постоянный коэффициент.

Из выражения (8.13) следует, что сосуд со свободным сливом име­ет нелинейную статическую харак­теристику (рис. 8.8). В неравновес­ном состоянии, в соответствии с уравнением (8.9), разность между притоком и стоком жидкости накап­ливается в сосуде. С учетом выражения (8.10) получаем

Второе слагаемое входит в нелинейной форме, поэтому дифферен­циальное уравнение (8.15) является нелинейным.

Ранее была сформулирована задача АСР: поддерживать выходной параметр в некоторой малой окрестности относительно заданного зна­чения с ошибкой, не превышающей + А. Следовательно, необходимо иметь математическую модель, описывающую с достаточной точно­стью поведение системы в этой малой окрестности. И математическая модель должна быть линейной. Достигается это путем линеаризации нелинейных уравнений.

Некоторые простые функции ( произведение, частные из деления переменных x,y и Vx) можно линеризировать , подставляя в них вместо переменных x,y выражения типа (x₀+ Выполнив математические операции, предписываемые линиризуемыми функциями и исключив из полученных зависимостей слагаемые, содержащие приращения второго и более высоких порядков, получают искомую линезированные произведения двух переменных производиться следующим образом:

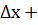₀y₀₊y₀ x₀+

Принимая во внимание, что x₀y₀=z₀

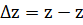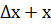₀=y_{0 0}

Аналогичным образом линеаризуют и уравнение динамики.

Линейные системы в статике и списываются линейными уравнениями. Такие же системы подчиняются принципу, или независимости возмущений. Он заключается в том что каждое входное величина системы создает свою составляющую выходной величины независимо от изменения других входных величин. Это позволяет рассматривать системы по каждому прохождения сигнала.

 

Пусть задана нелинейная, n раз дифференцируемая функция y = f(x). Разложим эту функцию в ряд Тейлора относительно точки с

координатами (y ₀,x₀):

И, отбросив нелинейные члены разложения, получим

Введя обозначения y- y₀=Аy и x-x₀=Аx, с учетом того, что

найдем линейное уравнение

где k постоянный коэффициент, характеризующий угол наклона каса­тельной к оси x.

Линейное уравнение (8.18) записано в отклонениях параметров и с заданной точностью соответствует исходной нелинейной функции в достаточно малом интервале относительно точки разложения.

Теперь разложим нелинейную функцию Q_ст(x) = рл/H в ряд Тей­лора относительно точки с координатами (Q _{ст ,} 0,H ₀) , удерживая два первых члена разложения:

и подставим результат в уравнение (8.15):

В результате получено приближенное обыкновенное дифференци­альное уравнение первого порядка, решив которое можно выполнить анализ динамических свойств сосуда со свободным сливом при малых возмущениях. Его можно записать в стандартной форме

Пример 2.Построить линейную математическую модель динами­ки теплообменника смешения (рис. 8.9).

Два потока жидкости с массовыми скоростями v1 и v₂, температурами t₁

и t₂ соответственно поступают в тепло­обменник смешения. Выходной поток

жидкости v = v₁ + v₂ нагревается до температуры t, которая является

выходным параметром.

Сформулируем допущения: температура t выходного потока равна температуре жидкости в теплообменнике вследствие полного переме­шивания; все потоки жидкости имеют теплоемкость c, и она остается

постоянной в заданном интервале температур.

В состоянии равновесия количество тепла, вносимое потоками Q_{1 0}

и Q₂ 0, равно количеству тепла, уносимого выходным потоком Q₀:

Это - уравнение статической характеристики теплообменника.

В неравновесном состоянии часть тепла расходуется на нагревание (охлаждение) жидкости массой G в теплообменнике:

Выполним очевидные преобразования и получим дифференциаль­ное уравнение динамики теплообменника смешения

Это уравнение относится к классу нелинейных, так как содержит нели­нейности типа произведения v •t, и его необходимо линеаризовать.

Запишем переменные величины, используя понятие отклонения

Из уравнения (8.30) вычтем уравнение (8.24):

Это обыкновенное дифференци­альное уравнение первого порядка, описывающее изменение температуры потока на выходе теплообменника под действием входных параметров с за­данной точностью относительно ста­ционарного состояния.

Линейные системы обладают свой­ством суперпозиции: реакция на сумму воздействий равна сумме ре­акций на каждое воздействие. Это свойство позволяет исследовать поведение систем под действием конкретного входного параметра, а остальные параметры обнуляются.

Уравнение (8.31) можно записать в стандартной форме:

Из анализа уравнения (8.32) следует, что теплообменник имеет че-тыре входных воздействия и один выходной параметр.