Пример расчета моды и медианы в дискретном ряду
| Распределение семей по числу детей (х) | Число семей (f) | Накопленные частоты (S) |
| Всего | - |
В интервальном вариационном ряду модой приближенно считается центральный вариант модального интервала, то есть того, который имеет наибольшую частоту. Это не обязательно середина модального интервала: только когда распределение симметрично или соседние интервалы не отличаются сильно частотами.
Мода рассчитывается в интервальном ряду по формуле:
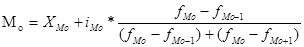(6.14) , где
XMo - нижняя граница модального интервала
iMo - величина модального интервала
fMo - частота модального интервала
fMo-1 - частота интервала, предшествующего модальному
fMo+1 - частота интервала, следующего за модальным
Мода несколько неопределённа, т.к. зависит от величины групп, от положения границ групп.
Медианой (Ме) в статистике называется варианта, которая находится в середине вариационного ряда, то есть делит численность упорядоченного вариационного ряда пополам. Для ранжированного ряда дискретного (построенного в порядке возрастания или убывания частот) с нечетным числом членов медианой будет варианта, расположенная в центре ряда:
В ранжированном ряду с четным числом медианой будет средняя арифметическая из 2-х смежных вариант: 1, 3, 4, 5, 7, 9 лет, следовательно, медиана равна 4,5 года (6 продавцов по стажу работы)
Медиана в дискретном ряду и медианый интервал в интервальном ряду находятся по данным о накопленных частотах. Медиана делит численность упорядоченного ряда пополам, значит находится там, где накопленная (кумулятивная) частота составляет половину или больше половины суммы частот, а предыдущая накопленная частота меньше половины численности совокупности.
В дискретном ряду, пример которого приведен в таблице 4, медиана - это 2 ребенка (åf/2 = 100,5). Накопление частот (числа семей) производится последовательным суммирование частот: 10семей, 40 семей, 115 семей, 160 семей и т. д. Число семей, равное 100,5 попадает в третью группу.
В интервальном вариационном ряду медиана рассчитывается по формуле:
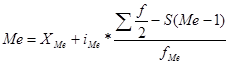(6.15) , где
XMe - начальное значение медианого интервала
SMe-1 - сумма накопленных частот до медианных интервалов
IMe - величина медианного интервала
fMe - частота медианного интервала
åf/2 - полусумма частот ряда
Медиана по своему положению более определена чем мода, так как по ее смыслу половина численности ряда имеет значение признака меньше, чем медианное, а другая половина – большее значение.
По данным примера интервального вариационного ряда, приведенного в таблице 2, определен средний уровень заработной платы: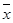 
= 1055,0руб. По приведенным методикам рассчитаем модальный уровень и медианный уровень заработной платы: Мо = 1070,83руб, Ме = 1069,0руб. Соотношение этих 3-х величин указывает направление и степень асимметрии распределения.
Если 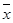, Мо, Ме совпадают - то группа данных чисел симметрична; 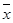>Ме при немногочисленной группе с очень высокими числами; 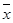<Ме - значит нет больших чисел, и данные концентрируются.
Если совокупность неоднородна, то мода определяется трудно. Она отчетливо выражена при однородности группы. Если имеется немногочисленная группа с высокими числами, т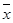о >Мо.
Величины, находящиеся на одной четверти и на трех четвертях расстояния от начала ряда называются квартилями, на одной десятой – децилями, на одной сотой – процентилями. Все они рассчитываются по формуле медианы с соответствующими изменениями. Так, при определении квартилей, берется в расчет 1/4, 2/4 или 3/4 суммы частот, нижняя граница и величина квартильного интервала, частота этого интервала. Сам квартильный интервал определяется по сумме накопленных частот, пересчитанной в проценты: 25 %, 50 %, 75 %. Аналогичная процедура применяется при расчете децилей (десятые части от 100 %) и процентилей (сотые части 100 %). Второй квартиль, пятый дециль и пятидесятый процентиль совпадают с медианой.
Контрольные вопросы.
1. В чем заключается сущность средней величины?
2. Какие виды средних величин применяются в статистике?
3. Как исчисляются средняя арифметическая простая и взвешенная?
4. Каковы основные свойства средней арифметической?
5.Чем отличается средняя гармоническая от средней арифметической?
6. Как рассчитывается средняя гармоническая взвешенная?
7. Какие еще виды средних величин Вы знаете?