Деление комплексных чисел

При делении комплексных чисел, заданных в тригонометрической форме имеем: z₁ = r₁ (cos j₁ + i sin j₁); z₂ = r₂ (cos j₂ + i sin j₂);

= = = =

=

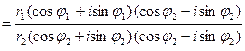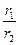
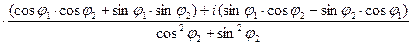Частное двух комплексных чисел есть такое комплексное число, модуль которого равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.

Пример для контроля усвоения: Даны два комплексных числа:

z₁ = 6 (cos 45⁰ + i sin 45⁰), z₂=2 (cos 15⁰ + i sin 15⁰).

Требуется найти: z₁ × z₂ и .

Ответы: z₁ × z₂ = 12 (cos 60⁰ + isin 60⁰); = 3 (cos 300 + i sin 300).

Вывод:Умножение (деление) комплексных чисел в тригонометрической форме сводится к перемножению (делению) их модулей и сложению (вычитанию) аргументов.

Формула Муавра. Извлечение корня