В) Задача Коши

Для уравнения n – го порядка формулируется следующим образом: найти решение дифференциального уравнения (4), удовлетворяющее начальным условиям:

= .

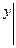
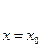
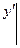
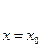
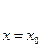
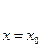Пример. Найти общее решение уравнения третьего порядка
y^III = 24x + 6 и выделить из него частное решение, удовлетворяющее начальным условиям:

.

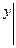
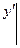
Решение. Так как y^III = (y^П)¢, то (y^II) ^I = 24х + 6.

Интегрируя, находим y^II = 12x² + 6x + c₁. Так как y^II = (y^I) ^I, то (y^I) ^I = 12x² + 6x + c₁ и, интегрируя ещё раз, получаем y^I = 4x³ + 3x² + c₁x + c₂.

Наконец, после ещё одного интегрирования получим общее решение:

y = x⁴ + x³ + + c₂x + c₃.

Выделим из него частное решение, удовлетворяющее данным начальным условиям.

Выпишем общее решение, первую и вторую его производные:

y = x⁴ + x³ + + c₂x + c₃;

y¢ = 4x³ + 3x² + c₁x + c₂;

y'' = 12x² + 6x + c₁

Подставим в эти соотношения начальные условия

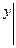
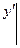
0 = c₃ Þ c₃ = 0;

0 = c₂ Þ c₂ = 0;

1 = c₁ Þ c₁ = 1.

Итак, частное решение, соответствующее данным начальным условиям, имеет вид:

y = x⁴ + x³ + x².

Таким образом, используя теорему Коши, решается задача Коши.