А) Общее, частное, особое решения

Занятие 2. Уравнения высших порядков

На данной лекции рассмотрим дифференциальные уравнения высших порядков, их общее, частное и особое решения, теорему и задачу Коши, а также дифференциальные уравнения, допускающие понижение порядка.

Дифференциальные уравнения высших порядков

а) Общее, частное, особое решения

Дифференциальное уравнение второго порядка связывает независимую переменную х, искомую функцию уи ее первую у' и вторую у^''производные.

Дифференциальное уравнение второго порядка в общем случае записывается в виде: F( x,y,y',y'' ) = 0 или, если это возможно, в виде, разрешенном относительно второй производной:

у'' = f (x,y,y').

Как и в случае первого порядка, для уравнения второго порядка могут существовать общее и частное решение.

Возьмём простейшее уравнение второго порядка: y'' = 2. (1)

Для его решения введём обозначение y^' = v (x). Тогда y'' = v¢, и уравнение (1) примет вид v¢ = 2. Отсюда следует, что v = 2x + c, или y^' = 2x + c.

Интегрируя ещё раз, найдём y = x² + c₁x + c₂. Полученное решение зависит от двух произвольных постоянных (общее решение). Геометрически это решение представляет множество парабол (интегральных кривых), причём через каждую точку плоскости, очевидно, проходит бесконечное множество парабол, имеющих в этой точке различные касательные. Для выделения из множества этих кривых какой – либо одной интегральной кривой, необходимо, кроме координат точки (x₀, y₀), через которую проходят параболы, дополнительно задать угловой коэффициент касательной, т.е. значение производной y^' в этой точке. Условия, с помощью которых из общего решения уравнений второго порядка выделяется частное решение, имеет вид:

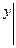
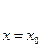
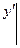
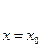
Они называются начальными условиями.

Определение. Дифференциальным уравнением n – го порядка называется уравнение, связывающее независимую переменную x, искомую функцию y и её производные y^', y^'',…,у⁽ⁿ⁾.

Символически дифференциальное уравнение n – го порядка можно записать так: F (x,у,у^',у^'',…,у⁽ⁿ⁾) = 0 или

F (x,у, 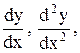…, 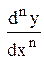) = 0 или

y⁽ⁿ⁾ = f(x,у,у',у'',……… y^{(n - 1)}).

Если искомая функция у = j(х) есть функция одного независимого переменного, то дифференциальное уравнение называется обыкновенным.

Определение. Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение

Примеры. 1) y^II + xy^I = 0 - уравнение второго порядка,

2) 5 xy - y^III = 8x - уравнение третьего порядка,

3) yy^I - 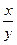= 0 - уравнение первого порядка.

Определение. Решением или интегралом дифференциального уравнения называется всякая функция y = j(x), которая будучи подставлена в уравнение, превращает его в тождество.

График решения называется интегральной кривой. Процесс нахождения решения называется интегрированием.

Общее решение уравнения n – го порядка зависит от n произвольных постоянных, т.е. является функцией вида:

y = j(x, c_1, c_2,….. c_n).

Решение дифференциального уравнения, получающееся из общего решения при конкретных значениях c_1, c_2,….. c_n называется частным решением.

Для того чтобы из общего решения уравнения выделить частное решение, задаются начальные условия. В случае уравнения n – го порядка начальные условия имеют вид:

.
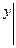
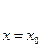
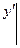
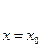
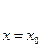
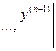
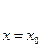