Б) Задачи, приводящие к ДУ
Физические задачи, приводящие к понятию дифференциального уравнения
А) Общие сведения о дифференциальных уравнениях
При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальныыми (термин принадлежит Г. Лейбницу, 1676 г.).
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Так, решением уравнения у' = f(x) является функция у = F(x) — первообразная для функции f(x).
Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае — ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение у'" — Зу" + 2 у = 0 — обыкновенное ДУ третьего порядка, а уравнение х2у' +5ху = у2 — первого порядка; у× z'х = х× z'y — ДУ в частных производных первого порядка.
Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ — интегральной кривой.
Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям.
б) Задачи, приводящие к ДУ
Задача 1 Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени.
Решение: Примем за независимую переменную время t, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией t, т. е. V = V(t). Для нахождения V(t) воспользуемся вторым законом Ньютона (основным законом механики): m× а = F, где а = V'(t) — есть ускорение движущегося тела, F — результирующая сила, действующая на тело в процессе движения.
В данном случае F = - kV2, к > 0 — коэффициент пропорциональности (знак минус заказывает на то, что скорость тела уменьшается). Следовательно, функция V = V(t) является решением дифференциального уравнения
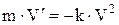 или
или 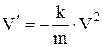 ,
,
здесь m – масса тела.
Как будет показано ниже (пример 5),
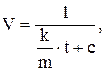
где с =const.