Функцияны зерттеу.

2.1 Функцияның өсу және кему аралықтары. Экстремумдар.

 

Теорема 5. болсын. Онда, егер

а) функциясы аралығында өссе (кемісе), онда аралығында ;

б) аралығында болса, онда функциясы аралығында өседі (кемиді).

Геометриялық тұрғыдан, функция өсетін болса, онда қисықтың жанамасы мен 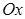өсінің арасындағы бұрыш -ден кіші, ал функция кемитін болса, онда бұл бұрыш -ден үлкен (16-сурет).

Теорема 6. (экстремумның бар болуының қажетті шарты).

нүктесі функциясының кризистік нүктесі болсын, ал - нүктесін ұстайтын интервал. Онда егер:

а) функциясы -де үзіліссіз және -де дифференциалданатын болса (ол нүктесінің өзі де болуы мүмкін), онда нүктесі максимум [минимум] (max [min]) нүктесі болады, егер нүктесінің сол жағынан оң жағына өткенде, таңба «+»-тен «-»-ке өзгеретін болса [«+»-тен «-»-ке өзгерсе];

б) және -де болса, онда нүктесінде функциясының максимумы [минимумы] (max [min]) бар болады, егер (17-сурет).

16-сурет

17-сурет

Ескерту 1. болсын. Онда функциясы аралығында ең үлкен және ең кіші мәнін не кризистік нүктелерде, не кесіндінің шеткі нүктелерінде қабылдайды.

 

2.2 Қисықтың ойыс және дөңестігі. Иілу нүктелері.

Анықтама 2. қисығы дөңес (ойыс) деп аталады, егер бұл қисықтың барлық нүктелері оның жанамаларының төменгі (жоғарғы) жағында орналасса.

 

18-сурет

Суретте аралығы , ойыс болатын аралығы. нүктесі қисығының иілу нүктесі деп аталады, егер оны басып өткенде қисығы ойыстығын дөңестікке немесе керісінше, дөңестігін ойыстыққа ауыстыратын болса.

Теорема 7. аралығында табылып, орындалатын болса, онда қисығы аралығында дөңес (ойыс).

Теорема 8. аймағында ( нүктесінің өзі болуы мүмкін), табылып, немесе анықталмаған болса және нүктесінен өткенде таңбасын өзгертсе, онда нүктесі иілу нүктесі.

2.3 Қисықтың асимптоталары

 

Анықтама 3. Түзу қисықтың асимптотасы деп аталады, егер қисықтың ағымдық нүктесінен түзуге дейінгі ара қашықтық, нүктесін шексіздікке жылжытқан сайын нөлге ұмтылатын болса.

а) б) в)

19- сурет

а) вертикаль асимптота, б) және в) көлбеу асимптота (19-сурет).

Қисық теңдеуімен берілсін. немесе ұмтылғанда функциясының шегі -ке ұмтылатын болса, онда түзуін вертикаль асимптота деп атаймыз.

түзуі көлбеу асимптота деп аталады, егер , теңдіктерімен анықталса.

 

2.4 Функцияның графигін зерттеудің жалпы жоспары.

1. Анықталу облысын және мәндерінің облысын табу.
2. Егер бар болса, үзіліс нүктелерін табу.
3. функциясының графигінің координат өстерімен қиылысу нүктелерін табу.
4. Функцияның жұптығын, тақтығын және периодтылығын зерттеу.
5. Өсу, кему аралықтарын және экстремумдарын табу.
6. Функцияның ойыс және дөңес болу аралықтарын, иілу нүктелерін табу.
7. Қисықтың асимптоталарын табу.
8. Зерттеудің нәтижесінде функцияның графигін салу.

Мысал 1. функциясын зерттеп, графигін салу.

1. Анықталу облысы: нүктесінен басқа барлық нақты сандар жиыны.

2. нүктесі функциясының үзіліс нүктесі:

,

нүктесі екінші түрдегі үзіліс нүктесі.

3. Егер болса, онда . аралығында , ал аралығында .

4. болғандықтан, функциясы жұп та емес, тақ та

емес және периодты емес.

5. Өсу, кему аралықтарын және экстремум нүктелерін табайық.

. Алдымен, кризистік нүктені табамыз:

а)

б) нүктесінде анықталмаған, ендеше .

Сонымен, кризистік нүктелер .

-тің таңбасы таңбасымен бірдей, яғни, теңсіздігін шешу жеткілікті. Бұл квадрат теңдеудің түбірлері 0 және 2, ал -тің коэффициенті оң сан. Сонымен,

20-сурет

а) болады, аралығында, яғни, аралығында кемиді;

б) болады және болса, яғни, және аралықтарында функциясы өседі;

в) нүктесінен өткенде таңбасын «+»-тен «-»-ке өзгертеді, нүктесінен өткенде

таңбасын «-»-тен «+»-ке өзгертеді, ал нүктесінен өткенде таңбасын өзгертпейді.

Сонымен, нүктесі , нүктесі нүктесінде экстремум жоқ.

6. Функцияның қисығының ойыс, дөңестігін және иілу нүктелерін табалық.

-тің таңбасы -дің таңбасымен бірдей. Ендеше, а) болады, аралығында, яғни, аралығында функциясының қисығы – дөңес; б) болады, аралығында, яғни, аралығында функциясының қисығы ойыс; в) нүктесінде анықталмаған және осы нүкте-сінде таңбасын «-»-тен «+»-ке өзгертеді. Ендеше, иілу нүктесі. Асимптоталарды табалық. а) вертикаль асимптота. б) көлбеу асимптота. , . Сонымен,

21-сурет

көлбеу асимптота.

8. Функцияның графигін тұрғызалық.

9-ші дәріс

Көп айнымалы функциялар.

 

Көп айнымалы функцияларды дифференциалдау туралы туралы сұрақтарды қарастыру кезінде жаңа ұғымдар пайда болады, біз жағдайын қарастырамыз, одан кейін оны жағдайлары үшін де қолдана аламыз.