Тамаша шектер

Практикада жиі кездесетін функциялардың шектеріне тоқталалық. - қандай да бір функция болсын және

(1)

теңдігі орындалсын.

1. Бірінші тамаша шек .

(2)

(2)-ші теңдіктен бірден төмендегі теңдіктерді алуға болады:

.

Ендеше, (1)-ші шарт орындалғандықтан, , , және - функциялары – эквивалентті функциялар.

Мысал 2.

а) . болғандықтан,(1)-ші шарт орындалады, онда

.

б) .

2. Екінші тамаша шек .

(3)

Мысал 3.

т.к. .

3. 4. 5. .

2. Үзіліссіз функциялар

-де қандай да бір нүктесінің маңайында функциясы анықталсын.

Анықтама 8. функциясы нүктесінде үзіліссіз деп аталады, егер а) нүктесінде анықталған болса;б) шегі табылса; в) .

Егер а), б), в) шарттарының тым болмағанда біреуі орындалмаса, онда нүктесі функциясының үзіліс нүктесі деп аталады.

 

Бір айнымалы үзіліссіз функцияларының қасиеттерін қарастырамыз. Егер функциясы нүктесінде үзіліссіз болса, онда теңдіктері орындалатындығы анық. Үзіліссіздіктің тағы бір анықтамасын берелік. нүктесінде айнымалысына өсімшесін береміз. Онда функция өсімшесін алады, әрі

Анықтама 9. функциясын нүктесінде үзіліссіз деп айтамыз, егер ол осы нүктеде анықталып және теңдігі орындалса.

Мысал 4. функциясын кез келген нүктесінде үзіліссіз екендігін дәлелде.

Шынында да, . Бұдан .

Қасиеттері:

1. Егер және функциялары нүктесінде үзіліссіз болса, онда осы нүктеде функциялары да үзіліссіз.

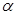2. Егер функциясы нүктесінде үзіліссіз, ал функциясы нүктесінде үзіліссіз болса, мұндағы , онда күрделі функциясы нүктесінде үзіліссіз.

 

2.1. Функцияның үзіліс нүктелері

Анықтама 10. функциясының үзіліс нүктесі жөнделетін үзіліс нүктесі деп аталады, егер шегі болып, бірақ та функциясы нүктесінде анықталмаған немесе болса.

Егер функциясы нүктесінде жөнделетін үзілісті функция болса, онда ол үзілісті жөндеуге болады. Яғни, анықталмаған, ал болса, онда деп алып, функциясын нүктесінде үзіліссіз қылып жіберуге болады.

Анықтама 11. нүктесі бірінші түрдегі үзіліс нүктесі деп аталады, егер табылып, тұрақты санға тең болса және теңдігі орындалса.

Мысал 5.

.

нүктесі бірінші түрдегі үзіліс нүктесі, себебі 2-сурет.

Басқа үзіліс нүктелерін екінші түрдегі үзіліс нүктесі деп айтамыз.

Мысал 6. . 3-сурет.

 

2.2 Кесіндідегі үзіліссіз функциялар

Анықтама 12. функциясы кесіндісінде үзіліссіз деп аталады, егер ол аралығындағы әрбір нүктеде үзіліссіз болса және теңдігі орындалса.

облысындағы үзіліссіз функциялардың класын деп белгілейміз.

Теоремалар. Егер , онда функциясы кесіндісінде шектелген. Егер , онда функциясы осы кесіндіде тым болмағанда бір рет ең үлкен мән мен ең кіші мән қабылдайды, яғни, және болсын, әрі болсын. Онда , мұндағы .

Салдар 1. Егер 3-теоремада , онда орындалатындай .

Е с к е р т у 3. бір айнымалы функцияның шектері (біржақты шектерден басқа) мен үзіліссіздігі туралы теоремалар мен қасиеттер көп айнымалы функциялар үшін де ақиқат

Өзін-өзі тексеруге арналған тест сұрақтары:

1. Шекті табыңыз:

[А][+]

[В]

[С] .

[Д]

[Е]

2. Шекті табыңыз:

[А]

[В] [+]

[С]

[Д] –1

[Е] 1

 

3. Шекті табыңыз:

[А] 2

[В]

[С] [+]

[Д] 0

[Е]

4. Шекті табыңыз:

[А] 3

[В] 1

[С] 4

[Д] [+] -3

[Е] –4

 

5. функциясының ұмтылғандағы шегі:

[А] тұрақты C-ға тең.

[В] нөлден өзгеше

[С] нөлге тең

[Д] -ге тең

[Е] [+] бірге тең

7-ші дәріс

Бір айнымалы функцияның туындысы. Лопиталь ережесі

 

Туынды

маңайында, нүктесін қоса алғанда, функциясы берілсін. нүктесінде аргументіне өсімшесін береміз. (оң немесе теріс). Онда .

Анықтама 1. Егер шегі табылса, онда оны нүктесіндегі функциясының туындысы деп айтамыз, немесе функциясы нүктесінде дифференциалданады деп айтамыз және былай белгілейміз: яғни,

(1)

Егер (1)-де және болса, онда (1)-ді нүктесіндегі оң жақ туындысы [ сол жақ туындысы] деп атаймыз. Егер және , онда .

Анықтама 2. функциясын кесіндісінде дифференциалданады деп айтамыз, егер оның аралығындағы әрбір нүктеде туындысы бар болса, ал және ұштарында сәйкесінше және табылса.

облысында дифференциалданатын функциялардың класын деп белгілейміз.

2. Туындының механикалық және геометриялық мағынасы

а) Механикалық. - нүктесінің қозғалу заңы болсын. нүктесінің -дан -ға дейінгі аралығындағы қозғалысын қарастыралық. Онда ал - орташа жылдамдық. Егер

,

шегі табылса, онда жолдың уақыт бойынша туындысы нүктесінің уақыт аралығындағы қозғалысының жылдамдығына тең.

12-сурет

б) Геометриялық. қисығында және нүктелерін қарастыралық. және екендігі анық. нүктесін қисықтың бойымен нүктесіне қарай жылжытамыз. нүктесінің орналасу аралығын белгілей отырып, қимасын аламыз. Онда болған жағдайда болатыны анық.

Анықтама 3. нүктесі қисықтың бойымен нүктесіне кез келген жағынан шексіз жақындағанда қимасының шектелген орны табылса, онда қисығына нүктесінде жүргізілген жанама деп аталады.

Егер қисықтың жанамасы бар болса, онда

.

Бұдан, нүктесінде дифференциалданатын функцияның осы нүктеде бұрыштық коэффициенті болатын жанамасы бар болады.

Мысал 1. функциясының нүктесіндегі жанамасының теңдеуін жаз.

а) . болғандықтан, жанаманың теңдеуі . -ті табалық:

б) . болғандықтан, және жанаманың теңдеуі . в)

13-сурет

14-сурет

Оң жақ жанамасы болады, яғни , ал сол жағынан жанамасы , яғни . Бұдан, нүктесінде берілген функцияның туындысы табылмайды, бұл функция нүктесінде үзіліссіз болғанның өзінде.

болатын нүктелер бұрыштық деп аталады.