Теоремалар.
1.  орындалуы үшін,
орындалуы үшін,  теңдігінің орындалуы қажетті және жеткілікті.
теңдігінің орындалуы қажетті және жеткілікті.
2. Егер  -да
-да  шектелген және
шектелген және  болса, онда
болса, онда
 ,
,  .
.
3. Егер  -да
-да  шектелген болса, онда
шектелген болса, онда 
 және
және  -
-  ұмтылғандағы шексіз кіші болсын және
ұмтылғандағы шексіз кіші болсын және  шегі табылсын, онда егер
шегі табылсын, онда егер
а)  - ақырлы болса, онда
- ақырлы болса, онда 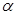 және
және  - бір ретті шексіз кіші функциялар, ал егер
- бір ретті шексіз кіші функциялар, ал егер  болса, онда
болса, онда 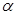 және
және  - эквивалентті
- эквивалентті  шексіз кіші функциялар.
шексіз кіші функциялар.
Ескерту 2.Шекті есептеу кезінде кез келген шаманы оған эквивалентті шамамен ауыстыруға болады.
б)  болса, -
болса, - 
 -ке қарағанда жоғары ретті шексіз кіші функция және оны былай жазамыз:
-ке қарағанда жоғары ретті шексіз кіші функция және оны былай жазамыз:  .
.
в)  болса, -
болса, - 
 -ке қарағанда жоғары ретті шексіз кіші функция.
-ке қарағанда жоғары ретті шексіз кіші функция.
Шексіз үлкен функциялар осыған ұқсас салыстырылады.
1.3. Анықталмағандықтар
 болсын.
болсын.  шегі табылсын делік.
шегі табылсын делік.
1.  - ақырлы. Бұл жағдайда,
- ақырлы. Бұл жағдайда,  және
және  функцияларының қандай болғанына
функцияларының қандай болғанына
қарамастан,  болады.
болады.
2. 
а)  . Онда
. Онда  .
.
б)  . Онда
. Онда  .
.
 боған жағдайда,
боған жағдайда,  және
және  функцияларының қалай берілгендігіне байланысты
функцияларының қалай берілгендігіне байланысты  анықталмаған болуы мүмкін, онда
анықталмаған болуы мүмкін, онда  ұмтылғанда
ұмтылғанда  функциясы
функциясы  түріндегі анықталмағандықты береді.
түріндегі анықталмағандықты береді.
Негізгі анықталмағандар:
 .
.