Кері матрица

Анықтама 10. шаршы (квадрат) матрицасы қайтымды емес немесе ерекше матрица

деп аталады, егер , кері жағдайда қайтымды немесе ерекше емес матрица деп аталады.

Теорема 2. Егер қайтымды матрица болса, онда матрицасы табылады және ол тек біреу ғана болып, төмендегі теңдік орындалады:

мұндағы – бірлік матрица.

- матрицасы кері матрица деп аталады және төмендегі формула бойынша есептелінеді

мұндағы , - матрицасының элементтерінің алгебралық толықтауышы.

Мысал 13. матрицасына кері матрицаны тап.

Шешуі.

(7 мысалды қара) болғандықтан, онда матрицасы қайтымды. Алгебралық толықтауыштарды табамыз.

Бұдан

2.3 Матрицаның рангі

Анықтама 11. матрицасының -ші ретті миноры деп матрицасының кез келген таңдап алынған баған мен жолдың элементтерінен құралған анықтауышты айтамыз.

Мысал 14.

матрицасы берілген.

Оның 2-ші ретті минорлары

және тағы басқалар.

3-ші ретті минорлары

Теорема 3. Егер -шы ретті минорлардың барлығы нөлге тең болса, онда -дан жоғарғы ретті барлық минорлар нөлге тең болады.

Анықтама 12. Матрицаның рангі деп нөлге тең емес минордың ең жоғарғы ретін айтамыз, ал кез келген -ші ретті нөлге тең емес минор базистік минор деп аталады.

Мысал 15. Матрицаларды көмкеру әдісі.

матрицасында -шы ретті миноры табылды делік. Осы минорын көмкеретін -ші ретті минорларды қарастырамыз. Егер ол минорлардың барлығы нөлге тең болса, онда . Егер минорын көмкеретін -ші ретті минорлардың ішінде тым болмағанда біреуі нөлге тең болмаса, онда осы нөлге тең емес минорды көмкеретін -ші ретті минорларды қарастырамыз, т.с.с.

2-ші ретті нөлге тең емес минор

белгілейік. Ендеше, . Енді -ні көмкеретін нөлге тең емес 3-ші ретті минорды іздейміз. Бұл минор

Бұдан, екендігі шығады.

Берілген матрицасының соңғы екі жолы тең болғандықтан, барлық 4-ші ретті минорлар нөлге тең болады. Дербес жағдайы, минорын көмкеретін минорлар нөлге тең. Ендеше, .

Е с к е р т у 3.Матрицаның рангі – осы матрицадағы сызықты тәуелсіз жолдардың (бағандардың) санына тең. 15 мысалда бұл сөйлемнің мағынасын былай түсінуге болады: матрицасының 1, 2, 3 жолдары сызықты тәуелсіз, ал матрицасының қалған жолдары (4 жол) 1, 2, 3 жолдардың сызықтық комбинациясы бойынша өрнектеледі.

Матрицаның экономикалық түсініктемесі.

Матрицаның көмегімен бірқатар экономикалық тәуелділіктерді жазуға болады.

Мысалы, экономиканық салалары бойынша ресурстарды үлестіру кестесі шартты бірлікпен берілген.

Ресурстар	Экономика саласы
өндіріс	ауыл шаруашылығы
Электр энергиясы	5,3	4,1
Еңбек	2,8	2,1
Су	4,8	5,1

Бұл кестені матрицалық формада

түрінде жазылады. Мысалға, өндіріс қанша электр энергиясын жұмсайтынын көрсетеді, ал ауыл шаруашылығына қанша электр энергиясының қажеттілігін білдіреді.

Өзін-өзі тексеруге арналған тест сұрақтары:

1.Екінші ретті анықтауыш тең:

[A][+]

[B]

[С]

[Д]

[Е]

2.Үшінші ретті анықтауыш тең:

[А]

[В][+]

С]

[Д]

[Е]

3. Егер анықтауыштың екі жатық жолдарын ауыстырсақ, онда оның мәні

[А]екі есе кемиді

[В]таңбасын өзгертпейді

[С][+] таңбасын өзгертеді

[Д]өзгермейді

[Е]екі есе өседі

3. Анықтауышты есептеңіз :

[А][+] 6

[В]18

[С] 12

[Д]0

[Е]1

4. Теңдеуді шешіңіз

[А] 0

[В] -4

С] 3

[Д] 4

[Е][+]-6

2-ші дәріс

N өлшемді векторлар. Сызықтық алгебралық теңдеулер жүйесі

1. N өлшемді векторлар.

Анықтама 1.Қандай да бір санның реттелген жиынтығы өлшемді вектор деп аталады, егер - компоненттері (вектордың координаттары).

Екі -өлшемді векторлар тең болады, егер олардың сәйкес компоненттері тең болса. векторы нөлдік вектор деп аталады.

Векторларға қолданылатын амалдар:

1. Векторларды қосу , :

2. Векторды санына көбейту:

Анықтама 2. векторлар жүйесі сызықты тәуелді деп аталады, егер

теңдігін қанағаттандыратын біруақытта нөлге тең емес сандары табылса, кері жағдайда жүйе сызықты тәуелсіз деп аталады.

Мысал 1. векторлары сызықты тәуелді, себебі

және векторлары сызықты тәуелсіз, себебі

Векторлар жүйесі сызықты тәуелді болса, онда жүйенің тым болмағанда бір векторын қалғандарының сызықтық комбинациясы түрінде өрнектеуге болады.

Q ке келген векторлар жүйесі болсын.

Анықтама 3. сызықты тәуелсіз векторлар жүйесі -дегі базисдеп аталады, егер

(1)

теңдігін қанағаттандыратын бір уақытта нөлге тең емес , сандары табылса. (1) формула векторының базисі бойынша жіктелуі деп аталады, ал векторының базисіндегі координаталары деп аталады. 1 мысалда және векторлары .

Теорема 1. өлшемді кез келген жүйе өлшемді векторлар жүйесінде сызықты тәуелді.

Анықтама 4.Векторлар жүйесінің рангі деп осы жүйенің базисіндегі векторлар санын айтамыз және ол осы жүйедегі сызықты тәуелсіз векторлардың ең үлкен санын айтамыз.

Теорема 2.Векторлар жүйесінің рангі жолдары осы жүйенің векторларының компоненттерінен құралған матрицаның рангіне тең.

Анықтама 5.Векторларды қосу және санға көбейту амалдары орындалатын өлшемді векторлар жиынын сызықтық кеңістігі деп атайды.

кеңістігінің рангі -ге тең, яғни, кеңістігіндегі кез келген сызықтық тәуелсіз векторлар базис құрайды және кеңістіктің өлшемідеп аталады.

2. Сызықтық алгебралық теңдеулер жүйесі.

Шешу тәсілдері.

Анықтама

6. белгісізі бар сызықтық алгебралық теңдеулер жүйесі деп мына түрде берілген жүйені айтамыз:

(2)

мұндағы - жүйенің коэффициенттері, ал - бос мүшелер, - белгісіздер.

7. сандары (2) жүйесінің шешімдері деп аталады, егер бұл сандарды теңдеудегі сәйкес белгісіздердің орнына қойғанда, осы жүйедегі тепе-теңдіктер орындалса.

8. (2) жүйесі үйлесімді деп аталады, егер оның тым болмағанда бір шешімі табылса, кері жағдайда жүйе үйлесімсіз деп аталады.

9. Үйлесімді (2) жүйесінің тек бір ғана шешімдері табылса, онда жүйе анықталған деп аталады, кері жағдайда жүйе анықталмаған деп аталады.

10. Егер , онда (2) жүйесін біртектес теңдеулер жүйесі деп атаймыз.

1-ші дәрісте айтылғандарды ескерсек, (2) жүйесін матрицалық түрде былай жазуға болады:

Кронекер-Капелли теоремасы.(2) жүйесі үйлесімді болуы үшін теңдігінің орындалуы қажетті және жеткілікті, мұндағы

(2) жүйесінің кеңейтілген матрицасы деп аталады.

(2) теңдеулер жүйесінің әрбір теңдеуі осы теңдеудің коэффициенттерімен бірмәнді анықталатындықтан, матрицасының жолдарын вектордың координаталары ретінде қарастыра отырып, - (2) жүйесінің сызықтық тәуелсіз теңдеулер санына тең болатындығына көз жеткіземіз.

Салдар 1. (2) жүйесі анықталған болады сонда және тек қана сонда ғана, егер

мұндағы - белгісіздер саны.

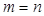және жағдайын қарастыралық. Онда салдар 1 бойынша (2) жүйесі анықталған және осы теңдеулер жүйесін шешу үшін келесі әдістерді қарастырамыз.

Крамер ережесі. (2) жүйесінің шешімдері мынадай формула арқылы анықталады:

мұндағы - анықтауыштағы -ші бағанды бос мүшелер бағанымен алмастырғаннан пайда болған анықтауыштар.

2. Матрицалық әдіс. болғандықтан

3. Гаусс әдісі (белгісіздерді біртіндеп жою әдісі). Элементар түрлендірулерді қолданып (2) жүйесін өзіне эквивалентті болатын диагоналдық жүйеге келтіреміз

(3)

одан кейін ең соңғы теңдеуден бастап біртіндеп жоғарылай отырып белгісіздерді анықтаймыз.

Мысал 2. Жоғарыда көрсетілген әдістерді қолданып, теңдеулер жүйесін шеш.

(4)

Шешуі:

Ендеше (4) жүйесінің тек бір ғана шешімі бар.

а) Крамер ережесі. табамыз.

бұдан

б) Матрицалық әдіс.(4) жүйесін түрінде жазамыз, мұндағы

1-ші дәрістегі 13-мысалдың нәтижесін қолдансақ,

Ендеше теңдігін қолданып матрицасын табамыз:

немесе .

Бұдан

в) Гаусс әдісі.Бірінші және екінші теңдеулердің орнын ауыстырамыз

Бірінші теңдеуді -2-ге көбейтіп, екінші теңдеуге қосамыз. Енді, бірінші теңдеуді -1-ге көбейтіп, үшінші жолға қосамыз. Сонымен, біз екінші және үшінші теңдеулердегі белгісізін жойдық:

Екінші жолды -ге көбейтіп, үшінші теңдеуге қосамыз. Сөйтіп, үшінші теңдеудегі белгісізін жойдық:

Енді төменнен жоғары қарай біртіндеп белгісіздерді табалық: үшінші теңдеуді шешіп , табылған мәнін екінші теңдеуге қойып, шешсек Табылған мәндерін бірінші теңдеуге қойсақ, болады.

2.1 Жалпы шешім туралы ұғым

Жалпы жағдайды қарастырамыз, жүйедегі теңдеулер саны белгісіздер санымен тең емес және

Онда біз былай жаза аламыз

(5)

(5)-тен шығатыны, соңғы теңдеуді алғашқы теңдеудің сызықтық комбинациясы ретінде жаза аламыз. Соңғы теңдеуді жүйеден алып тастап, ал қалған теңдеулердегі белгісіздерін теңдіктің оң жағына шығара отырып, (2) жүйеге эквивалентті теңдеулер жүйесін аламыз:

(6)

мұндағы айнымалылары базистік айнымалылар деп аталады, ал айнымалылары еркін айнымалылар деп аталады. (5)-тен, егер айнымалыларын ғана белгісіздер деп алатын болсақ, онда (6) жүйесінің тек бір ғана шешімі бар екендігі шығады және белгісіздерін еркін белгісіздер арқылы өрнектей аламыз. (6) жүйесінің шешімін, яғңи базистік айнымалылардың еркін айнымалылар арқылы өрнектелуін (1) жүйесінің жалпы шешімі деп атаймыз.

Мысал 3. Үйлесімділікке зертте және үйлесімді болған жағдайда теңдеулер жүйесінің жалпы шешімін тап

(7)

, .

болғандықтан (оқырман өз бетімен есептеуіне болады), теңдеулер жүйесі үйлесімді және

Ендеше, 1-ші және 2-ші теңдеулерді ғана қалдырып, қалған теңдеулерді алып тастауға болады. және айнымалыларын теңдіктің оң жағына шығара отырып, бірінші теңдеуде айнымалысын жойсақ, онда

(8)

аламыз. (8) (7) теңдеулер жүйесінің жалпы шешімі, - базистік айнымалылар, - еркін айнымалылар.

Е с к е р т у 1. (7) теңдеулер жүйесін бірден Гаусс әдісімен де шешуге болады. Гаусс әдісімен шешу кезінде есептеу барысында (7) теңдеулер жүйесінің үйлесімді ме жоқ па екендігі анықталады, үйлесімді болған жағдайда жүйенің жалпы шешімі табылады.

Бірінші теңдеуді -2-ге көбейтіп, екінші теңдеуге қосамыз. Енді бірінші теңдеуді -1-ге көбейтіп, төртінші теңдеуге қосамыз:

2-ші теңдеуді 3-ші және 4-ші жолдарға қосамыз

яғни, (7) теңдеулер жүйесінің жалпы шешімін таптық, - базистік айнымалылар, - еркін айнымалылар. Егер бірінші теңдеуден -ті тауып, оны екінші теңдеуге қоятын болсақ, онда (8) жалпы шешімін аламыз. Бұл істелінген әрекет еркін айнымалысын базистік айнымалыға айналдыру деп аталады.

2.2 Біртектес сызықтық теңдеулер жүйесі

Мынадай сызықтық теңдеулер жүйесін қарастыралық

(10)

(10) теңдеулер жүйесі үнемі үйлесімді болатыны анық, себебі оның тривиалды шешімі бар. Салдар 1-ден (10) теңдеулер жүйесінің нөлге тең емес шешімдері болуы үшін, теңсіздігінің орындалуы қажетті және жеткілікті екендігі шығады.

Мысал 4. Біртектес теңдеулер жүйесін шеш:

Гаусс әдісімен шығарамыз. Екінші және үшінші теңдеулердегі айнымалысын жоямыз

Өзін-өзі тексеруге арналған тест сұрақтары:

1. Теңдеулер жүйесін шеш

[А]

В][+]

[С]

[Д]

[Е]

2. Теңдеулер жүйесін шеш

[А]

В]

[С][+]

[Д]

[Е]

3. Теңдеулер жүйесін шеш

[А]

[В]

[С]

[Д][+]

[Е]

4. Теңдеулер жүйесін шеш

[А]

[В]

[С]

[Д]

[Е][+]

5. Теңдеулер жүйесін шешу керек

[А]

[В]

[С][+]

[Д]

[Е]

3-ші дәріс

Векторлар. кеңістігі. Векторлардың скаляр, векторлық және

аралас көбейтіндісі

1. кеңістігіндегі векторлар.

2. Тікбұрышты декарттық координаталар жүйесі

3. Векторларды скаляр көбейту

4. өлшемді кеңістіктегі нүкте ұғымы

2-ші дәрісте енгізілген өлшемді векторлар ұғымы мен жазықтығы мен кеңістігіндегі геометриялық объект түрінде қарастырылатын вектор ұғымын байланыстырамыз. Ол үшін вектор және оған қолданылатын амалдар ұғымын енгіземіз.

1. кеңістігіндегі векторлар.

Анықтама:

1.Вектор деп басы нүктесі, ұшы нүктесі болатын бағытталған кесіндісін айтамыз.

2. векторының ұзындығы (модулі) деп кесіндісінің ұзындығын айтамыз.

3.Векторлар тең деп аталады, егер олардың ұзындықтары тең болса және бірдей бағытталған болса.

1-сурет
Анықтама 3-тен кез келген векторды өзіне-өзін параллель жылжытуға болатындығы шығады.

4.Бір түзудің бойында немесе параллель түзулердің бойында жататын векторлар, коллинеар (параллель) векторлар деп аталады және былай белгіленеді .

5.Егер және нүктелері беттесетін болса, онда немесе - нөлдік вектор.

6.Егер , онда - бірлік вектор.

7. векторлары компланар деп аталады, егер олар біз жазықтықта жатса не параллель жазықтықтарда орналасқан болса.

8. векторының өсіне проекциясы деп шамасын айтамыз, мұндағы өсінің бағыты мен векторының арасындағы бұрыш.

2-сурет
Егер және нүктелері сәйкесінше нүктелерінің өсіне түсірілген проекциясы болса, онда болатыны анық.

9. санының векторыныа көбейтіндісі деп ұзындығы -ға тең болатын және болғанда бағыты векторымен бағыттас, ал болғанда векторына қарама-қарсы бағытталатын векторды айтамыз.

Төмендегі қорытындылар бірден анықтамадан шығады:

а) Егер болса, онда теңдігі орындалатын саны табылады;

б) Егер және олар қарама-қарсы бағытталған болса, сонымен қатар, болса, онда немесе .

10.Екі вектор параллелограммдар ережесі бойынша қосылады. ?

3-сурет
Осыдан -де кез келген екі коллинеар емес вектор базис құра алады, ал -те үш компланар емес вектор базис құра алады.

2. Тікбұрышты декарттық координаталар жүйесі

нүктесі арқылы өтетін өзара перпендикуляр үш түзудің боынан кеңістігінде базис құрайтын сәйкесінше бірлік векторларын таңдап аламыз. түзулерін координат өстері деп, ал нүктесін – координаттың бас нүктесі деп атаймыз.

кеңістіктегі кез келген нүкте болсын, ал нүктелері - нүктесінің координат өстеріне түсірілген проекциялары.

4-сурет Онда - абсцисса - ордината - аппликата - базисінде жіктелуі, ал - векторының координаталары [ нүктесінің координаталары] және былай белгіленеді: .

және векторлары берілсін. Онда

, мұндағы - тұрақты сан.

.

Біз 2-ші дәрісте енгізілген вектор ұғымына қайтіп келдік. кеңістігіндегі нүктесі мен векторының арасында өзара бірмәнді сәйкестік бар екенін ескерген жөн.

Анықтама 15. векторының бағыттаушы косинустары деп сандарын айтамыз, мұндағы - векторының сәйкесінше координат өстерімен жасайтын бұрыштары. ?

Бағыттаушы косинустар .

Бұдан

Е с к е р т у 1.Үш координата ( -де екі координата) векторды бірмәнді анықтайтындықтан, көптеген геометриялық есептерді аналитикалық түрде шығаруға болады (координаталардың жиынтығы арқылы).

Мысал 1.Кесіндіні берілген қатынаста бөлу. кесіндісін және нүктесін қарастырамыз, онда

. (3)

нүктесінің координаталарын табалық.

5-сурет

болсын. Онда

, онда

Немесе .

Дәл солай,

3. Векторларды скаляр көбейту

Анықтама 16. және векторларының скаляр көбейтіндісі деп, мынадай формула бойынша есептелетін шаманы айтамыз:

. (4)

болғандықтан, онда . ?

Қасиеттері: 1. Егер

, онда

Скаляр көбейтудің координаталық формадағы өрнектелуін табалық. болсын. Онда екенін ескерсек, . Немесе

(5)

üҚ о р ы т ы н д ы.Векторларды скаляр көбейтудің көмегімен мыналар анықталады:

1. Екі вектордың перпендикулярлығы

(6)

2. Векторлар арасындағы бұрыштың косинусы

(7)

3. Бір вектордың екінші векторға түсірілген проекциясы

(8)

Е с к е р т у 2. Жоғарыда көрсетілген барлық анықтамалар мен формулалар -де де орынды. Тек қана координатасын алып тастау қажет.

4. өлшемді кеңістіктегі нүкте ұғымы

- ағымдық нүкте, - таңдап алынған нүкте, - және нүктелерінің ара

қашықтығы болсын. теңсіздігін қанағаттандыратын нүктелер жиынын нүктесінің аймағы деп атаймыз.

Келесі жағдайларды қарастырамыз.

1. Бірөлшемді кеңістік ( сандық түзуі). -те орналасқан кез келген нүктенің орны бір координата арқылы бірмәнді анықталады, және нүктелері үшін , ал дегеніміз интервалы.

2. Екіөлшемді кеңістік ( жазықтығы). -те орналасқан кез келген нүктенің орны екі координата арқылы бірмәнді анықталады, және нүктелері үшін , ал жазықтығындағы центрі нүктесі, радиусы болатын шеңбер.

3. Үшөлшемді кеңістік ( кеңістігі). -те орналасқан кез келген нүктенің орны үш координата арқылы бірмәнді анықталады және және үшін , ал кеістігіндегі центрі нүктесі, радиусы болатын шар.

Дәл солай осы процессті жалпылайтын болсақ, нүктесі өлшемді кеңіс-тіктегі координаталары болатын нүкте, мұндағы және нүктелері арасындағы ара қашықтық мына формула бойынша анықталады:

ал центрі нүктесі, радиусы болатын өлшемді шар.

Өзін-өзі тексеруге арналған тест сұрақтары:

1.:Векторлардың скаляр көбейтіндісі

[А]

[В]

[С][+]

[Д]

[Е]

2. векторлардың скаляр көбейтіндісі мынаған тең

[А]

[В]

[С]

[Д] [+]

[Е]

3. мен векторларының ортоганалдығы белгісінің қажетті және жеткілікті шартын көрсет

[А]

[В] сан

[С]

[Д]

[Е] [+]

4. мен векторлардың коллинеарлық белгісінің қажетті және жеткілікті шартын көрсет

[А] [+]

[В]

[С]

[Д]

[Е]

5.Егер болса, есепте:

[А] [+] 3

[В] 0

[С] –3

[Д] 4

[Е] 5

4-ші дәріс

Сызықтық геометриялық объектілер

Сызықтар, беттер және олардың теңдеулері.

Жазықтықтағы түзу.

Жазықтық.

4. Кеңістіктегі түзу

Сызықтар, беттер және олардың теңдеулері.

Объект деген сөзді жазықтықтағы сызықтар, кеңістіктегі сызықтар мен беттер деп түсінеміз.

Анықтама:

1. Объект деп әрқайсысы осы объектінің мінездемелік қасиеттерін қанағаттандыратын нүктелердің геометриялық орны (н.г.о.).

2.Математикалық қатынастар арқылы немесе объектінің нүктелерінің координаталары арасындағы қатынастар арқылы жазылған объектінің мінездемелік қасиеттерін объектінің теңдеуі немесе объектінің теңдеулер жүйесі деп атаймыз.

Мысал 1. Центрі координатаның бас нүктесінде орналасқан радиусы жазықтықтағы шеңбер – объект. Мінездемелік қасиеті: шеңбердің барлық нүктелері осы шеңберінен бірдей қашықтықта орналасқан. Егер координаталардың бас нүктесі, ал шеңбердің ағымдық (кез келген) нүктесі болса, онда немесе шеңбердің мінездемелік қасиетінің математикалық түрде жазылуы. Ықшамдай келе, объектінің теңдеуін аламыз .

Объектпен таныса келе мынадай сұрақтар туындайды:

1. Берілген мінездемелік қасиеті бойынша объектінің теңдеуін құру.

2. Берілген объекттің теңдеуі бойынша, теңдеудің әртүрлі параметрлік мәндерінде объектіні зерттеу.

Мысал 2.