Распределение молекул газа, находящегося в состоянии равновесия, по направлениям движения
Рассмотрим газ находящийся в состоянии равновесия. При этом он занимает объем V и содержит N молекул. При отсутствии внешних сил молекулы газа распределяются равномерно по объему V и движутся хаотически не имея преимущественного направления. Если провести сферу радиуса R вокруг объема V и в произвольный момент времени продолжить направления скоростей движения всех молекул до пересечения с этой сферой, то вся сфера покроется точками в местах этих пересечений. Причем из-за отсутствия преимущественного направления в движении молекул (равновесие) поверхностная плотность этих точек r = N /4pR2 будет постоянна по всей сфере в любой момент времени.
Выберем на сфере произвольную элементарную площадку dS Тогда количество точек, оказавшихся на этой площадке
dN = NdS /4pR2= Ndw /4p (1.3.1)
где dw = dS /R2 - телесный угол, под которым видна площадка из
центра сферы. (Полный телесный угол, стягиваемый сферой w = ∫ dw = ∫ dS/R2 =4pR2/R2=4p)
Соотношение (1.3.1) можно представить в виде:
dN / N = dw /4p (1.3.2)
Левая часть равенства (1.3.2) представляет собой отношение числа молекул dN, направления скоростей которых заключены и телесном угле dw, к общему числу молекул и при большом N равна вероятности того, что "взятая наугад" молекула в газе имеет направление скорости, заключенное в телесном угле dw Формула (1.3.2) выражает закон равновероятности направлений движения молекул в равновесном состоянии газа.*
* Основные сведения из теории вероятностей даны в Приложении А. Нумерация формул в Приложении А дается по форме (А.5), что означает: формула 5 Приложения А.
Р и с. 7
Найдем дифференциал площади dS в сферической системе координат. Для этого проведем через ось Z (рис. 7) две бесконечно близкие плоскости под углами j и j + dj к плоскости XOZ. Они пересекут сферу по окружностям O΄BO΄΄ и O΄CO΄΄ радиуса R. Далее проведем два конуса с углами 2q и 2(q+dq) при вершине O , которые пересекут сферу по окружностям С΄СС΄΄и В΄DВ΄΄. В результате пересечения четырех указанных окружностей получается элемент сферы, (на рис.7 заштрихован) площадь которого
dS =BC·BD, (1.3.3)
где BC = ABdj=R sinq dj , BD =R dq
Подставляя последние величины в формулу (1.3.3), получим выражение для бесконечно малой площади в сферической системе координат:
dS=R 2sinq dq dj (1.3.4)
Из выражений (1.3.4) и (1.3.1) находим число частиц, которые имеют направления, определяемые сферическими углами, лежащими в интервалах от j до j + dj и от q до q + dq :
dNq,j=N sinq dq dj /4p (1.3.5)
Если разделить обе части соотношения (1.3.5) на объем V, занимаемый газом, то получим
dnq,j=n sinq dq dj /4p (1.3.6)
где dnq,j=dNq,j /N - число молекул в единице объема, которые имеют направления вектора скорости близкое к направлению, определяемому углами j и q , n=N/V - число молекул в единице объема с любыми направлениями движения.
Примеры
1. Найти полный телесный угол, стягиваемый любой замкнутой
поверхностью, окружающей начало координат.
Решение. Подставим в выражение dw=dS/R2 , определяющего бесконечно малый телесный угол, величину dS из формулы (1.3.1), получим
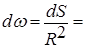sinq dq dj
Интегрируя по всем возможным углам (j изменяется от 0 до 2p, q - от 0 до p), получим
2. В некотором сферическом объеме газ находится в равновесии и содержит N=2,7·1025 молекул. Построим конус с вершиной в центре этой сферы и углом раствора в один стерадиан. Какое число N1 молекул из общего числа N имеют направления скоростей, заключенных в этом пространственном угле?
Решение: Из формулы (1.3.2), путем интегрирования находим искомое число
