Виды средних и способы их вычисления

В статистике применяются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя гео­метрическая, средняя квадратическая, средняя кубическая и др.

Перечисленные средние относятся к классу степенных сред­них и объединяются общими формулами (при различных значе­ниях к):

Простая степенная средняя 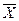= 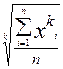, (9)

 

Сложная степенная средняя 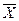= k 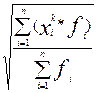, (10)

 

Где 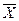- среднее значение исследуемого явления;

k - показатель степени средней;

х – текущее значение (вариант) осредняемого признака;

n – число единиц совокупности;

f - число единиц в i-той группе.

В зависимости от значения показателя степени k различают следующие виды степенных средних:

при k = 1 – средняя арифметическая;

при k = 2 – средняя квадратическая;

при k = 3 – средняя кубическая.

Свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистикеправилом мажорантности средних.

Вид средней для анализа определяется в каждом конкретном случае исходя из характера имеющихся данных.

Кроме степенных средних в статистике используются структурные средние величины, в качестве которых рассматриваются мода и медиана.

 

Наиболее распространенным в статистике видом средних величин является средняя арифметическая, представляющая собой частное от деления суммы индивидуальных значений признака на их количество.

Средняя арифметическая бывает простой и взвешенной.

Средняя арифметическая простаяприменяется в тех случаях, когда каждое индивидуальное значение признака встречается один или одинаковое число раз.

Формула:

 

(11)

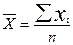
Где: Х1 – индивидуальные значения варьирующего признака:

n – число единиц совокупности.

Пример 7. Имеется информация о стаже пяти рабочих ,при этом стаж первого рабочего составил 5 лет, второго – 7, третьего – 4, четвертого – 10, пятого – 12 лет.

Определить средний стаж работы.

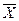= 5 + 7 + 4 + 10 + 12 = 7,6 лет.

Среднюю арифметическую взвешеннуюрассчитывают в тех случаях, когда отдельные значения исследуемой совокупности встречаются не один, а несколько, причем неодинаковое число раз, то есть представляю собой ряд распределения.

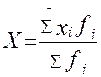, (12)

Где: f – веса (частоты повторения одинаковых признаков);

∑xf – сумма произведений величины признаков на их частоты;

∑f – общая численность единиц совокупности.

Пример 8. Рассчитать среднюю заработную плату работников в бригаде из 20 человек, оплата труда которых варьируется от 5800 до 14400 рублей.

Таблица 6

Заработная плата работников бригады

Заработная плата, руб. ( )						Итого
Число работников, чел. ( )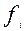

 

Применяя формулу средней арифметической взвешенной, получаем:

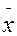= 5800 * 2 + 7100 * 11 + 8500 * 5 + 10500 * 1 + 14440 * 1 = 7857 руб.

2 + 11 + 5 + 1 + 1

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы):

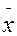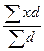= (13)

В статистической практике бывают случаи, когда при вычислении средней имеются данные об индивидуальных значениях признака (х) и его общем объеме в совокупности (W = x*f), но не известны частоты проявления признака (f). В таких случаях среднее значение признака вычисляется по формуле средней гармонической, которая представляет собой величину, обратную средней арифметической из обратных значений вариант.

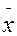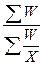= , где w = x * f. (14)

Пример 9. Требуется определить средний размер двух видов вклада в банке в октябре и ноябре по данным таблицы 4.

Таблица 7

Информация о вкладах в банке для расчета средних значений

Вид вклада	Октябрь	Ноябрь
Число вкладов f, тыс.	Средний размер вклада х, руб.	Сумма вкладов w, млн. руб.	Средний размер вклада х, руб.
До востребования			4,07
Срочный			3,87

 

Для расчета среднего размера вклада в октябре применяем формулу средней арифметической взвешенной:

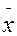= 350 * 10000 + 400 * 8000 = 372,22 руб.

10000 + 8000

В ноябре известен средний размер вкладов каждого вида, а количество вкладов неизвестно, но имеются данные об общих суммах их вкладов.

Путем деления сумм вкладов W каждого вида на их средний размер вклада Х можно определить веса – число вкладов f по их видам, а затем определить средний размер вклада по двум видам по формуле средней арифметической взвешенной. Однако, если в расчете использовать среднюю гармоническую взвешенную, то отпадает необходимость предварительных расчетов весов – размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу.

Средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной:

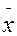гарм. = 4 070 000 + 3 870 000 = 7 940 000 = 397 руб.

4 070 000 + 3 870 000 20 000

370 430

Средняя геометрическаяприменяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическаяисчисляется извлечением корня степени n из произведений отдельных значений – вариантов признака Х:

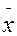геом = 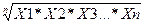, (15)

где n – число вариантов.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяются средняя квадратическая (например, для вычисления средней величины стороны n квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны n кубов).

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

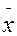кв = ; (16)

Средняя квадратическая взвешенная:

 

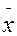кв = 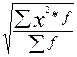, где f – веса. (17)

Средняя кубическая рассчитывается аналогично.

Средняя квадратическая и кубическая имеют ограниченное применение в практике статистики. Больше используется средняя квадратическая, но не из самих вариантов Х, а из их отклонений от средней (х - 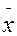) при расчете показателей вариации.

В статистике употребляются еще две разновидности средних величин, которые вытекают из характеристики статистических рядов и не являются результатом каких-либо алгебраических действий – это структурные средние: мода и медиана.

Модой называется величина, которая чаще всего встречается в статистическом ряду. Ее обозначают Мо.

Медиана – это среднее значение показателя в ранжированном ряду. Ее обозначают Ме.

Важное свойство медианы – это сумма отклонений вариантов признака от медианы, есть величина наименьшая:

 

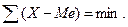
В интервальном вариационном ряду моду определяют по формуле:

Мо = Хо + i f2-f1 (18)

(f2-f1)+(f2-f3),

 

Где: Хо – нижняя граница модального интервала;

i – величина модального интервала;

f 1; f 2; f 3 – частоты предмодального, модального и послемодального интервалов.

Для расчета медианы в интервальном ряду используют формулу:

Ме = Хо + (19)

Где: Хо – нижняя граница медианного интервала;

i – величина медианного интервала;

∑f – сумма частот ряда;

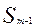- сумма накопленных частот до медианного интервала;

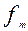- частота медианного интервала.

Пример 10:

Размер расхода на услуги в месяц, руб.	Тыс. чел.
До 300	495,8
300,1 - 600	759,3
600,1 - 900	267,4
900,1 - 1200	81,1
1200,1 и выше	27.1
Итого	1630,7

 

Мода расходов на услуги составит:

Мо = 300 + 300 759,3 – 495,8 = 405 руб.

(759,3 – 495,8) + (759,3 – 267,4)

Медиана составит:

1630,7

Ме = 300 + 300 * 2 - 495,8 = 426,3 руб.

759,3

Полученный результат говорит о том, что из 1630,3 тыс. человек половина тратит на услуги 426,3 рубля.