Лекция № 5

Уравнение переноса примесей в турбулентной атмосфере.
Анализ отдельных членов уравнения

 

1. Общий вид уравнением турбулентной диффузии примесей

2. Адвективный приток примеси

3. Конвективный приток примеси

4. Приток примеси под влиянием горизонтального турбулентного обмена

5. Приток примеси под влиянием вертикального турбулентного обмена

6. Учет захвата и вымывания примеси каплями и кристаллами облаков и осадков

 

1 Общий вид уравнением турбулентной диффузии примесей.Уравнение переноса (притока) примеси в турбулентной атмосфере, называемое также уравнением турбулентной диффузии примесей, имеет следующий вид (рассматриваются средние значения концентрации, скорости движения и др.)

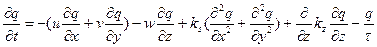(1)

Выполним качественный анализ уравнения переноса примесей, позволяющий оценить знак различных членов в правой части (1), а вместе с этим и тенденцию изменения концентрации примесей во времени под влиянием различных факторов. Отметим, что горизонтальные составляющие скорости переноса примеси и, v совпадают с составляющими скорости ветра. Что касается вертикальной составляющей w, то для газообразных примесей, а также мелких (легких) жидких и твердых примесей, радиус частиц которых меньше 1 мкм, она практически равна вертикальной скорости движения воздуха. Однако в случае крупных (тяжелых) примесей (радиус частиц больше 1 мкм) под составляющей w в уравнении (1) следует понимать алгебраическую сумму вертикальной скорости движения воздуха w_a и средневзвешенной (по массе) скорости падения 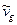частиц примеси под влиянием силы тяжести, но с учетом, конечно, силы трения:

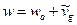, (2)

при этом под 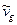понимается абсолютная величина (модуль) скорости падения частиц, которая всегда направлена по вертикали вниз, поэтому она и вычитается. Вертикальная же скорость положительна (w_a > 0) при восходящем движении воздуха и отрицательна (w_a <. 0) при нисходящем.

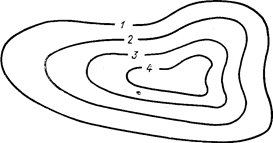
Рисунок 1 - Поле концентрации примесей в горизонтальной плоскости

 

Согласно уравнению (1), концентрация примеси в фиксированной точке пространства (дq/дt — локальная производная во времени) изменяется со временем под влиянием следующих факторов.

2 Адвективный приток примеси – первое слагаемое в правой части (1). Для оценки этого фактора необходимо иметь данные о концентрации примеси во многих точках города и скорости ветра. Нанеся данные измерений q на карту, проводим изолинии концентрации (q=const). Изолинии эти имеют, как правило, эллипсоидальную форму, при этом максимум концентрации (при осреднении ее за достаточно большой интервал времени – декаду, месяц, сезон) находится, как правило, вблизи центра города (рис. 1). Наряду с основным максимумом q наблюдается несколько вторичных максимумов. Если ось х направлена по касательной к линии тока, которую следует также провести на карте, то, согласно данным рис. 1, на наветренной стороне города и> 0, v=0 и дq/дx>0. Таким образом, адвективный приток примеси здесь меньше нуля ( 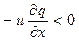), а концентрация примеси под влиянием этого фактора со временем убывает (дq/дt < 0).

На подветренной стороне города, согласно данным рис. 1, и > 0, v=0 и дq/дx < 0. Здесь, таким образом, адвективный приток примеси больше нуля, а ее концентрация со временем возрастает.

 

3 Установившееся распределение примеси по высоте Конвективный приток примеси – второе слагаемое в правой части (1). Для оценки этого фактора необходимо знать вертикальные профили концентрации примеси и скорости w.

В общем случае концентрация загрязняющих атмосферу веществ является сложной функцией координат и в каждой точке пространства изменяется под влиянием рассмотренных выше факторов во времени. Исследовать эту зависимость концентрации от координат и времени на основе уравнения (1) можно в общем случае лишь с помощью численных методов с последующей реа­лизацией построенного решения на современных ЭВМ. К тому же для построения замкнутого решения уравнение (1) следует дополнить уравнениями движения (для определения и и v), неразрывности (для определения w_a), баланса турбулентной энергии (для k_z), движения частиц примеси и капель облаков и осадков (для определения 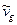и τ). Необходимо также привлечь ряд полуэмпирических соотношений – функции распределения частиц примеси, а также капель облаков и осадков по размерам; формулу, связывающую коэффициент ks с характеристиками поля ветра; ряд формул теории подобия или эмпирических выражений, устанавливающих связи между параметрами вертикального обмена и термодинамическими величинами.

В этой общей постановке исследование и количественная оценка загрязнения атмосферы примесями различного происхождения далека от завершения. Однако к настоящему времени выполнено большое число оценок загрязнения атмосферы для некоторых частных случаев, которые получаем на основе различных предположений об источниках примесей, характере движения, коэффициентах уравнений и др.

Рассмотрим один из таких частных случаев. С этой целью осредним уравнение (1) за достаточно большой интервал времени (декада, месяц, сезон, год) и по большой площади, например по всему городу. Тогда можно считать близкими к нулю:

а) левую часть уравнения – процесс загрязнения воздушного бассейна города установившийся (dq/dt=0); б) адвективный приток примеси ( 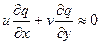), поскольку этот приток имеет разные знаки в различных частях города и меняет знак во времени в одной и той же точке, прежде всего, под влиянием смены направления ветра.

С учетом того что горизонтальная диффузия учитывается с помощью формулы (2), уравнение (1) для этого частного случая запишем в виде

(3)

При этом мы также предполагаем, что коэффициенты уравне­ния k_z, w, τ равны некоторым осредненным по времени и площади значениям, поэтому они вынесены из-под знака осреднения. Однако коэффициенты k_z, w и τ в уравнении (3) являются функциями высоты. Поэтому решение даже этого упрощенного уравнения без специальных допущений о виде функциональной зависи­мости коэффициентов от высоты можно построить лишь с помощью численных методов. Чтобы получить решение уравнения (3) в виде, выражающемся через известные функции, дополнительно предположим: в) скорость w не зависит от высоты и равна некоторому среднему по всему пограничному слою значению: w=w=const; г) в приземном слое толщиной h=50—100 м, в котором существенно изменение k_z с высотой, мала роль вымывания примесей осадками или радиоактивного распада, поскольку толщина этого слоя мала по сравнению со всем пограничным слоем. Что касается коэффициента турбулентности k_z, то, как установлено многочисленными исследованиями, в частности с привлечением теории подобия и размерности, коэффициент этот в приземном слое всегда растет (в непосредственной близости к земной поверхности –линейно) с увеличением высоты. Выше приземного слоя k_z практически не зависит от z.

Малые высоты. В случае тяжелой (радиусом в несколько десятков микрометров) примеси концентрация таких примесей всегда убывает с высотой. Однако в случае газообразных, а также легких твердых и жидких примесей, концентрация таких примесей не падает, а растет с высотой. Но в таких барических системах следует учитывать захват и вымывание примеси облаками и осадками, поскольку они здесь всегда наблюдаются.

Большие высоты (верхняя, экмановская, часть пограничного слоя). Концентрация тяжелой (достаточно крупной) примеси (v_g>0), а также концентрация любых примесей при w_a < 0 (антициклоны и гребни) всегда падает с высотой, асимптотически приближаясь к нулю при z→∞.

Турбулентный обмен в свою очередь интенсивен в тех случаях, когда наблюдается сильный ветер или термическая стратификация приземного слоя неустойчивая—вертикальный градиент температуры γ= – дТ/дz больше сухоадиабатического γ_а, а в насыщенном воздухе – влажноадиабатического градиента 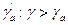или 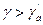или когда сильно шероховатая земная поверхность.

Поскольку на значительных высотах концентрация примеси при малых значениях параметра а повышена (см. рис. 2), то как из физических представлений, так и из результатов расчета следует, что концентрация примеси на малых высотах, в частности в непосредственной близости к земной поверхности, понижена, однако при том непосредственном условии, что масса примесей, поступающих из источников, во всех случаях сохраняется постоянной.

 

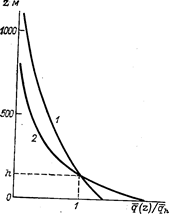
Рисунок 2 - Распределение нормированной (на q_h) концентрации примесей по высоте при малых (1) и больших (2) значениях параметров а и δ.

 

Рисунок 3 - Распределение концентрации примесей по высоте при сильно (1) и
слабо (2) развитом турбулентном обмене.

 

При больших значениях параметров а и δ концентрация примеси быстро падает с высотой, вследствие чего ее содержание мало на значительных высотах и велико на малых, в частности вблизи земной поверхности. Большие значения а и δ отмечаются в тех случаях, когда слаборазвит турбулентный обмен (мала скорость ветра, устойчивая, особенно инверсионная, термическая стратификация приземного слоя: 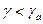или 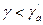; мала шероховатость земной поверхности) или велики размеры частиц примеси или наблюдаются сильные нисходящие движения (скорость их w_a < 0 и велика по модулю — в мощных антициклонах). Типичные кривые распределения над городом концентрации загрязняющих веществ по высоте при малых и больших значениях параметров а и δ приведены на рис. 2, 3.

Из приведенных рассуждений следует: по сравнению с некоторым средним уровнем, наблюдаемым в данном городе, высокие уровни загрязнения на малых высотах создаются или при слабом ветре, или при сильно устойчивой (инверсионной) стратификации, когда разность температур воздуха у земной поверхности (Т_о) и на некоторой высоте, например 500 м (T₅₀₀), отрицательна: ΔТ==Т₀-Т₅₀₀ < 0. Такая стратификация чаще наблюдается ночью и зимой, чем днем и летом, или при антициклонической метеорологической обстановке. Нередко все эти факторы действуют одновременно, и тогда возникает наиболее тяжелая обстановка – содержание загрязняющих веществ на малых высотах особенно велико, их концентрация может во много раз превышать предельно допустимую концентрацию (ПДК).

На больших высотах при этих условиях содержание примесей понижено, толщина аэрозольного облака z* над городом минимальна (оно прижато к земле).

4 Приток примеси под влиянием горизонтального турбулентного обмена– третье слагаемое в правой части (1). Этот фактор всегда приводит к распространению (диффузии) примеси на то или другое расстояние от ее источников, в частности, в окрестностях города. Хотя и построены решения уравнения (1), учитывающие влияние горизонтальной диффузии, однако более целесообразно, в соответствии с опытными данными, описывать распределение примеси по горизонтали, обусловленное турбулентностью, с помощью нормального закона (формулы Гаусса), т. е. представляя q (x, у, z, t) в виде

, (4)

где 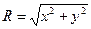– расстояние турбулентной частицы (моля) от оси z, σ_r—среднее квадратическое отклонение этого расстояния, q*(z,t)—осредненная по горизонтальной площади S, теоретически бесконечно большой, концентрация примесей на данной высоте z в момент времени t.

Легко видеть, что максимальное значение концентрации, равное q*(z,t), определяемое выражением (4), наблюда­ется в начале координат (при х=у=0). Поле концентраций симметрично относительно этого начала. С увеличением расстояния R от начала координат концентрация убывает по экспоненциальному закону, асимптотически приближаясь к нулю при R→∞.

Сравним распределение q(x, у, z, t) по горизонтали при двух значениях стандарта σ_r, например σ’_r и σ’’_r, при этом σ’_r < σ’’_r. При R=0 концентрация q(0, z, t) в первом случае, когда турбулентный обмен менее интенсивен (вследствие этого σ’_r мало), больше, чем во втором (при σ’’_r):

q'(0, z, t)>q"(0, z, t).

 

Такое же неравенство сохраняется при малых значениях R. Однако поскольку при увеличении R концентрация во втором случае убывает медленнее (велико σ’’_r), чем в первом, то на больших расстояниях от центра города, в соответствии с физическими представлениями, соотношение между концентрациями q'(R, z, t)<q"(R, z, t)

противоположно наблюдаемому при малых значениях R (рис. 4). Более того, составив отношение q"(R, z, t)/q' (R, z, t), убеждаемся в том, что на очень большом расстоянии от центра города это отношение неограниченно растет при увеличении R.

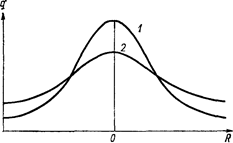
Рисунок 4 - Распределение концентрации примесей по горизонтали при слабо (1) и сильно (2) развитом турбулентном обмене

5 Приток примеси под влиянием вертикального турбулентного обмена – четвертое слагаемое в правой части уравнения (1). В случае высотного источника примесь поступает к земной поверхности под влиянием переноса ее турбулентными молями. С усилением неустойчивости возрастает интенсивность турбулентного об­мена, а вместе с ним и концентрация примеси вблизи земной поверхности. Такое заключение справедливо лишь для высотных источников. Для низких (в том числе наземных) источников зави­симость концентрации от стратификации противоположна, наи­большая концентрация примесей в этом случае наблюдается при устойчивом (особенно, инверсионном) распределении температуры с высотой.

 

6 Учет захвата и вымывания примеси каплями и кристаллами облаков и осадков.Пятое слагаемое в правой части уравнения (1) описывает убыль (отток) примеси вследствие захвата примеси каплями и кристаллами облаков, туманов и осадков, а также радиоактивного распада примеси, если она радиоактивна. Под влиянием этого фактора, а также падения частиц в поле силы тяжести происходит самоочищение атмосферы. Все другие факторы лишь перераспределяют примесь в атмосфере. Если действует только пятый фактор, то уравнение (1) принимает вид

.

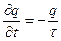Интегрируя это уравнение при начальном условии q=q₀ при t=0, получаем q(t)=q₀exp(-t/τ).

Таким образом, при t=τ концентрация (q(τ)=q₀/е, т. е. за время, равное τ, концентрация убывает в е=2,72... раз. Эти рассуждения выясняют физический смысл времени жизни примеси τ.

Выше уже указано, что при циклонической обстановке, когда w_a > 0, необходимо учитывать влияние захвата и последующего вымывания загрязняющих веществ каплями и кристаллами облаков и осадков. Этот процесс в конечном счете приводит к самоочищению атмосферы. Газообразные примеси, в первую очередь диоксид серы, реагируют с каплями, превращаясь в жидкие примеси, и с ними оседают на земную поверхность.

Легко видеть, что с учетом вымывания концентрация примеси, как тяжелой, так и легкой, всегда убывает с высотой не только при нисходящих, но и при восходящих вертикальных движениях воздуха в циклонах.

Концентрация любой примеси (легкой и тяжелой) всегда падает с высотой при любой синоптической обстановке. Однако скорость убывания q(z) при увеличении высоты существенно различна в областях пониженного и повышенного давления.

Например, концентрация примеси убывает в е =2,72 раз по сравнению со значением ее при z=h при подъеме всего лишь примерно на 200 м в антициклоне и более чем на 750 м в циклоне. Из этого следует, что общая метеорологическая обстановка оказывает существенное влияние на уровень загрязнения атмосферы: при антициклонической обстановке концентрация примесей повышена вблизи земной поверхности и понижена в верхней части пограничного слоя; циклоническая обстановка сопровождается снижением уровней загрязнения на малых высотах и ростом их на больших К тому же следует иметь в виду, что в антициклонах чаще, чем в циклонах наблюдается инверсионная стратификация и более слабые ветры.

По формулам можно оценить высоты верхней границы облака примесей.

Общий вывод сводится к тому, что метеорологические условия оказывают существенное (нередко определяющее) влияние на уровни загрязнения атмосферы вблизи земной поверхности, на распределение концентрации примесей в пространстве и изменение во времени.

Остановимся еще на учете адвективного притока примеси. Легко видеть, что на наветренной стороне города концентрация примеси под влиянием адвекции падает с высотой быстрее, чем в случае отсутствия адвекции, в то время как на подветренной стороне города этот процесс идет медленнее.